高校化学の問題演習
令和6年6月30日
中和反応の量的関係
※宇都宮大学の入試問題です。
次の文章を読んで、以下の問い(1)~(7)に答えよ。
炭酸水素ナトリウムと、ある濃度の塩酸を用いて、以下に示す化学反応における質量変化の測定を行った。
【実験操作】
i) ビーカーに塩酸50.0mLを量り取り、電子天びんで、このビーカーと塩酸の合計の質量を測定したところ$m_0$(g)であった。
ii) i)の塩酸に、炭酸水素ナトリウムを一定量ずつ加え、炭酸水素ナトリウムを加えることで起こる変化が完全に終わった後に溶液とビーカーを合わせた質量$Z$(g)を電子天びんで測定した。以上の操作を繰り返し行った。なお、質量測定を行うとき、ビーカーの中には固体は存在しなかった。
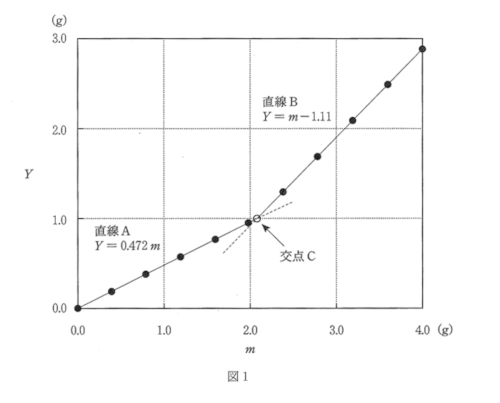
上記の実験操作ii)において、加えた炭酸水素ナトリウムの全量$m$(g)と、$Z$(g)から$m_0$(g)を引いた値$Y$(g)との関係をグラフにすると図1の結果が得られた。この結果を線で結ぶと、直線Aおよび直線Bが得られ、$Y$と$m$の関係は図中に示す関係式で表されることがわかった。なお、炭酸水素ナトリウムの式量は84.0とし、操作中は、温度は一定で、水の蒸発はなく、発生する気体は全てビーカーから大気中に出てしまうものとする。
(1) 塩酸(塩化水素)に炭酸水素ナトリウムを加えたときに起こる化学反応の化学反応式を書け。
(2) この測定で、$Y$と$m$の間に直線関係が2つ現われる理由について述べよ。また、【実験操作】ii)で起こる化学反応において、図1の交点Cは何と呼ばれるのか答えよ。
(3) 図1から、【実験操作】i)で量り取った塩酸が全て反応するために必要な炭酸水素ナトリウムの質量(g)を、小数点以下3桁を四捨五入して小数点以下2桁まで求めよ。なお、解答では考え方も記せ。
(4) 【実験操作】i)で量り取った塩酸の中に存在していた塩化水素の物質量(mol)を、小数点以下4桁を四捨五入して小数点以下3桁まで求めよ。なお、解答では考え方も記せ。
(5) この実験で用いた塩酸のモル濃度(mol/L)を、小数点以下3桁を四捨五入して小数点以下2桁まで求めよ。解答では考え方も記せ。
(6) 交点Cまでに加えた炭酸水素ナトリウムの量$m$(g)と、気体の発生量$M$(g)を表す関係式を直線AとBの傾きから求めよ。
(7) この測定結果から、【実験操作】ii)で発生する気体の分子量を求めることができる。(6)で求めた関係式を用いて、発生する気体の分子量を、小数点以下2桁を四捨五入して小数点以下1桁まで求めよ。解答では考え方も記せ。
令和6年3月31日
分子の存在
※宮崎大学の入試問題です。
次の文を読み、下記の設問に答えよ。
1803年にドルトンは、気体の性質やラボアジエが発見した (a) ,プルーストが発見した (b) を説明するために原子説を発表した。ゲーリュサックは、1808年に発見した (c) を原子説で説明しようと試み、「すべての気体は、同温・同圧・同体積中に同数個の原子を含む」という仮説をたてたが、説明しようとすると矛盾が生じる。この矛盾を解決するため1811年にアボガドロは、
(1) 単体の気体は、複数の原子が結合した分子からなる。
(2) すべての気体は、種類にかかわりなく、同温・同圧・同体積中に同数個の分子を含む。
という仮説を提唱した。
1860年にカニッツァーロは、アボガドロの仮説を真であると考えることにより、各元素の原子についてその質量の比が求まり、その結果(1)の分子説が自然に導かれることを示した。すなわち、水素を例にとると、まず同温・同圧のもとで水素ガスの密度と気体状の水素化合物$X$(水素とある元素の化合物)の密度を測定する。(2)の仮説より、水素化合物の密度を水素ガスの密度で割った値は、水素ガスの分子1個の質量を1としたときに、水素化合物$X$の分子1個の質量がその何倍であるかを示す値$y$となる。
一方、この水素化合物$X$を分析し、その質量にしめる水素の質量百分率を求めることにより、値$y$にしめる水素の量(この分子$X$1個に含まれる水素原子の質量が水素ガスの分子1個の質量と比べたときに、その何倍であるかを示す値)が計算できる。例えば、いろいろな質量の水素と酸素を化合させて生じた水の質量との関係から、水の質量にしめる水素の質量の割合が求められる。したがって、この関係を用いると、水素化合物$X$の$z$〔g〕を燃焼させたときに生じた水の質量から$z$〔g〕に含まれる水素の質量が求められる。ほかの多くの水素化合物について、同じようにしてその物質の質量に占める水素の質量百分率を求め、比較することによって水素ガスの分子1個の質量が水素の原子1個の質量の何倍であるかが求められ、水素分子が何個の水素原子でできているかが決定できる。
問1 文中の空欄 (a) ~ (c) に、最も適当な化学史上の重要な法則を答えよ。
問2 文中の下線部に述べられている実験において、水素,酸素,水のうち少なくとも2つの物質の質量が測定されれば十分である。3つの物質の質量を測定しなくてもよい理由を述べよ。
問3 下の表に0℃,1atm(1013hPa)のもとでの気体状水素化合物の密度を水素ガスの密度で割った値$D$とその化合物中での水素の質量の百分率を示した。このデータのみに基づき、カニッツァーロの方法で、水素ガスの分子は水素原子2つが結合してできたものであることを導け。
塩化水素 |
硫化水素 |
アンモニア |
|
$D$ |
18.23 |
17.12 |
8.560 |
質量百分率 |
2.74 |
5.87 |
17.60 |
問4 問3の結果を基に考えたとき、塩化水素は、同温、同圧の塩素ガスと水素ガスから生成する。そのときの体積比は、塩素ガス,水素ガス,塩化水素ガスが1:1:2である。塩素分子が水素と同じように塩素原子2個でできていると考えると、先の表のデータから、塩素原子1個の質量は水素原子1個の質量の何倍と考えられるか、有効数字3桁で答えよ。(半角のみで入力すること)
令和5年12月24日
理想気体と実在気体
※神戸大学の入試問題です。
※入力は次の指示にしたがってください。
- 入力は、半角で入力すること。記号を答える問題は、半角アルファベットの小文字のみ入力すること。
- かけ算の「かける」という記号のみ全角の×で入力すること。
- 累乗は、たとえば「3の2乗」なら3^2のように、^を使って入力すること。
次の文章を読んで、問1~5に答えなさい。計算のために必要であれば、次の値を用いなさい。
気体定数:\( 8.31×10^3 \)Pa・L/(K・mol)
絶対零度:-273℃
理想気体1molの温度が$T$(K)で、圧力が$P$(Pa),体積が$V$(L),気体定数が$R$であるとき、
\( \fbox{A} = RT \) …(1)
が成り立つ。式(1)では、分子自身には大きさが無く、分子間に引力が働かないと仮定されている。しかしながら、実在する気体では、この仮定は成り立たない。これに対して、ファンデルワールスは分子自身の体積と分子間に働く引力を考慮して式(1)を補正し、実在気体によくあてはまる状態方程式を導き出した。
今、1molの実在気体について考えてみる。実在気体の体積$V_r$は、その分子自身の体積の影響を考慮し、分子自身の体積の効果を表す正の定数$b$を用いることで、
$V_r$ = ア
と表すことができる。
また、実在気体1molについて体積が小さくなるほど、分子間に働く引力は\( \fbox{B} \)なる。この分子間に働く引力により、実在気体の圧力$P_r$は理想気体の圧力に比べて\( \fbox{C} \)なるため、分子間に働く引力の効果を表す正の定数$a$を用いることで、$P_r$は
$P_r$ = イ
と表すことができる。
以上より、1molあたりの実在気体について$P_r$,$V_r$,$a$,$b$を用いることで、
\( \fbox{D} = RT \) …(2)
が導き出される。この式(2)はファンデルワールスの状態方程式とよばれ、$a$,$b$はファンデルワールスの定数とよばれている。
理想気体1molでは、式(1)の右辺と左辺との比は、常に1になる。この比は圧縮因子と呼ばれ、$Z$で表す。
\( \displaystyle Z = \frac{\fbox{A}}{RT} = 1 \)
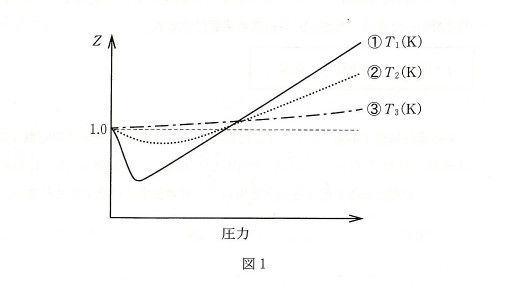
しかし、実在気体については、式(1)の仮定が成り立たないため、$Z$は1からずれることが知られている。図1は、ある実在気体の温度$T_1$(K)および$T_2$(K),$T_3$(K)における、圧力と$Z$との関係を表したグラフである。ただし、図1の温度および圧力範囲では気体状態であることは確認されている。
問1 空欄 ア , イ にあてはまる式を以下の(a)~(j)の中から選び、記号で答えなさい。
(a) \( V+b \) (b) \( V-b \)
(c) \( V×b \) (d) \( V÷b \)
(e) \( b÷V \) (f) \( \displaystyle P+\frac{a}{V_r^2} \)
(g) \( \displaystyle P-\frac{a}{V_r^2} \) (h) \( P×aV_r^2 \)
(i) \( P+aV_r^2 \) (j) \( P-aV_r^2 \)
問2 空欄\( \fbox{A} \)~\( \fbox{D} \)にあてはまる最も適切な語句または式を記入しなさい。
問3 図1より、曲線①~③は圧力が高いところで$Z$ = 1からずれ、そのずれの程度は温度により異なる。このときの温度$T_1$(K),$T_2$(K),$T_3$(K)の関係を表す最も適切なものを以下の(a)~(f)の中から選び、記号で答えなさい。
(a) \( T_1<T_2<T_3 \) (b) \( T_1>T_2>T_3 \)
(c) \( T_2<T_3<T_1 \) (d) \( T_2>T_3>T_1 \)
(e) \( T_3<T_1<T_2 \) (f) \( T_3>T_1>T_2 \)
問4 問3の解答の理由について、以下の3つの語句をすべて使用して、40字以内で説明しなさい。ただし、句読点も字数に含める。
分子間力 熱運動 高温
問5 ある実在気体1mol,27℃,1Lにおけるファンデルワールスの定数$a$と$b$の値が、それぞれ\( a = 1.41×10^5 \)(Pa・L2)/mol2,\( b = 3.91×10^{-2} \)L/molのとき、この実在気体の圧力を式(2)を用いて、有効数字3けたで答えなさい。
令和5年9月17日
分子の立体構造と極性
※お茶の水女子大学の入試問題を参考に作られています。
一般に、分子を構成する原子数が3以上の分子では、図3に示すように様々な立体構造が考えられる。各分子の安定な立体構造を知ることは、分子の性質を理解するために必要である。これまでの研究から、分子の立体構造形成に重要な、次の二つの法則が知られている。
【法則1】各原子周りの電子対(共有電子対および非共有電子対)は反発し合い、電子対は互いにできるだけ遠くの位置を占める。
【法則2】非共有電子対は共有電子対に比べ空間的な広がりが大きいため、共有電子対と非共有電子対間の反発は、共有電子対間の反発より強い。
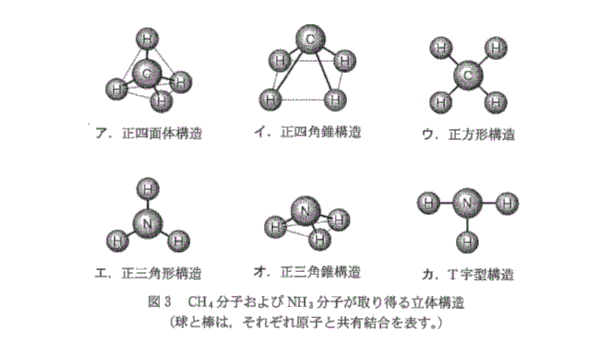
(i) $\ce{CH4}$分子および$\ce{NH3}$分子の立体構造を図3から選び、記号(ア~カ)で答えよ。(全角のみで入力すること)
(ii) $\ce{CH4}$分子の$\ce{H-C-H}$結合角と$\ce{NH3}$分子の$\ce{H-N-H}$結合角の大きさの関係はどのようになるか。理由とともに答えよ。
(iii) $\ce{CH4}$分子と$\ce{NH3}$分子は、それぞれ、極性をもつか否か。その判断理由も答えよ。
令和5年6月18日
ペプチドのアミノ酸配列
※広島大学の入試問題です。
※必要があれば、次の原子量を使用してください。
$\ce{H}$:1 $\ce{C}$:12 $\ce{O}$:16
次の文章を読み、問1~問5の答えを記入せよ。
ペプチドAは下の表に示す$α$-アミノ酸のうち、異なる4つの$α$-アミノ酸が直鎖状に縮合した化合物である。表に各$α$-アミノ酸名と等電点を示す。
$α$-アミノ酸 |
等電点 |
グリシン |
5.97 |
アラニン |
6.00 |
グルタミン酸 |
3.22 |
システイン |
5.07 |
フェニルアラニン |
5.48 |
リシン |
9.74 |
ペプチドAのアミノ酸配列を決定する目的で実験a)~f)を行った。以下に実験a)~f)の内容と結果を示す。
a)ペプチドAをある条件で部分的に加水分解すると、3種類のペプチドB,C,Dといくつかの$α$-アミノ酸に分解された。
b)ペプチドB,C,Dを分離し、それぞれの水溶液に水酸化ナトリウム水溶液と硫酸銅(Ⅱ)水溶液を加えて呈色反応を行った結果、いずれのペプチド水溶液においても呈色は観察されなかった。
c)分離したペプチドBとCそれぞれの水溶液に濃硝酸を加えて加熱すると、いずれの水溶液も黄色に変化し、冷却後アンモニア水を加えると橙黄色に変化した。
d)分離したペプチドCとDそれぞれの水溶液に水酸化ナトリウム水溶液を加えて加熱後、酢酸鉛(Ⅱ)水溶液を加えると、いずれの水溶液からも黒色沈殿が生じた。
e)ペプチドAをアミノ酸にまで完全に加水分解し、得られた4種類の$α$-アミノ酸をpH = 7.4の緩衝液中で電気泳動により分析した結果、陰極側へ移動する$α$-アミノ酸が存在することがわかった。
f)ペプチドDをアミノ酸にまで完全に加水分解すると複数の$α$-アミノ酸が得られた。これらのうち、一つの$α$-アミノ酸のメタノール溶液に濃硫酸を加えて加熱後、炭酸水素ナトリウムで中和すると分子量103の化合物が生成した。
問1 実験b)の呈色反応の名称を記せ。また、この実験b)の結果からわかることを簡潔に説明せよ。
問2 実験c)の呈色反応の名称を記せ。また、この反応により検出される$α$-アミノ酸を表から一つ選び、名称を記せ。(全角のみで入力すること。)
問3 実験d)の反応で検出される$α$-アミノ酸を表から一つ選び、名称を記せ。また、この反応で生じる黒色沈殿を化学式で記せ。(カタカナは全角で、アルファベットは半角で入力すること。)
問4 実験e)の陰極側に移動する$α$-アミノ酸を表から一つ選び、名称を記せ。また、この$α$-アミノ酸が陰極側に移動する理由を簡潔に説明せよ。
問5 ペプチドAを構成する$α$-アミノ酸の正しい配列を以下の(ア)~(コ)の中から一つ選び、記号で記せ。(全角のカタカナのみで入力すること。)
(ア) リシン―システイン―フェニルアラニン―アラニン
(イ) アラニン―システイン―フェニルアラニン―グルタミン酸
(ウ) アラニン―グリシン―グルタミン酸―リシン
(エ) グリシン―システイン―グルタミン酸―リシン
(オ) リシン―アラニン―システイン―フェニルアラニン
(カ) アラニン―グルタミン酸―グリシン―フェニルアラニン
(キ) システイン―アラニン―リシン―フェニルアラニン
(ク) アラニン―システイン―フェニルアラニン―リシン
(ケ) フェニルアラニン―グリシン―アラニン―グルタミン酸
(コ) グルタミン酸―グリシン―リシン―システイン
