高校数学(3・C)の問題演習
最大・最小の利用
※弘前大学の入試問題です。
$a$,$b$は定数で、$a>0$とする。
関数 \( \displaystyle f(x) = \frac{x-b}{x^2+a} \)の最大値が\( \displaystyle \frac{1}{6} \),最小値が\( \displaystyle -\frac{1}{2} \)であるとき、$a$,$b$の値を求めよ。
無理方程式の実数解
次の$x$についての方程式がある。この方程式の実数解の個数を調べなさい。
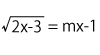
部分積分法
※宮崎大学の入試問題です。
次の定積分の値を求めよ。
(半角数字で答えること。文字が入る場合、文字については全角にすること。)
(1)\( \displaystyle \int_0^1 x・e^xdx \)
(2)\( \displaystyle \int_0^π x・\sin{x}dx \)
複素数平面と正三角形
※県立広島大学の入試問題です。
$α$、$β$は2次方程式\( x^2-2x+4 = 0 \)の異なる2つの虚数解とする。
(1)\( α^2+αβ+β^2 \)の値を求めよ。(半角で入力すること)
(2)複素数平面上の3点$A(α)$、$B(β)$、$P(z)$が正三角形の頂点になるような$z$を求めよ。(すべて半角で入力すること)
無限等比級数の和と公比
ある無限等比級数の和を$A$、その各項の3乗を項とする無限等比級数の和を$B$とする。$A$、$B$それぞれが次の値のとき、はじめの級数の各項の4乗を項とする無限等比級数の和は、いくらになるか求めなさい。ただし、はじめの無限等比級数は初項、公比ともに実数である。
(答えが分数になるときは、「(分子)/(分母)」の形で入力し、数字は半角で入力すること)
\( A = 3 \)
\( \displaystyle B = \frac{108}{13} \)
