問題ページにもどる

この問題のポイント

（１）\( x^2-2x+4 = 0 \)の虚数解を求めて、それを代入して、という方法でももちろん求めることはできます。
ただし、代入する式には、2乗があったりして少し計算が面倒なので、ここではもう少し簡単に計算できる方法で求めていきましょう。

$α$、$β$は両方とも\( x^2-2x+4 = 0 \)の解なんですから、解と係数の関係により、
\( \displaystyle α+β = -\frac{-2}{1} = 2 \)
\( \displaystyle αβ = \frac{4}{1} = 4 \)

よって、
\( α^2+αβ+β^2 \)
\( = (α+β)^2-αβ \)
\( = 2^2-4 \)
= 0

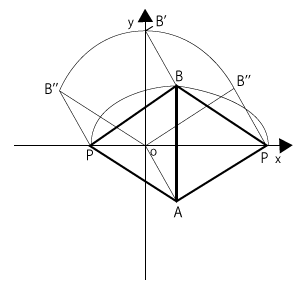
（２）正三角形とは、1つの角が60°で、辺の長さはどれも同じ三角形です。ということは、右図で示しているように、$P(z)$は$A(α)$を中心に$B(β)$を60°、または-60°だけ回転させた点だということになります。

ただし、複素数平面上では、回転は原点を中心にして考えたほうがわかりやすいので、$A$を原点$O$に平行移動させて考えましょう。もちろん、$A$のみを平行移動だけさせてはいけませんから、$B$も同じように平行移動させます。その点が右図の$B'$です。

そして、$B'$を$O$のまわりに60°、または-60°だけ回転させた点を右図のように$B''$とします。そのようにしてから、$O$を$A$に平行移動させて戻し、点$B''$も同じように平行移動させて戻した点が$P$だと考えればいいのです。

以上の点を1つ1つ考えていくと、

\( B'…β-α \)

\( B''…(β-α)\{\cos(±60°)+i\sin(±60°)\} \)

\( P(z)…(β-α)\{\cos(±60°)+i\sin(±60°)\}+α \)
\( \displaystyle = (β-α)\frac{1±\sqrt{3}i}{2}+α \)

ここで\( x^2-2x+4 = 0 \)を解き、\( α = 1-\sqrt{3}i \)、\( β = 1+\sqrt{3}i \)とすると、

$z$
\( \displaystyle = \{1+\sqrt{3}i-(1-\sqrt{3}i)\}・\frac{1±\sqrt{3}i}{2}+1-\sqrt{3}i \)
\( \displaystyle = 2\sqrt{3}i・\frac{1±\sqrt{3}i}{2}+1-\sqrt{3}i \)
\( = \sqrt{3}i・(1±\sqrt{3}i)+1-\sqrt{3}i \)

よって、これを展開すると、
\( \sqrt{3}i-3+1-\sqrt{3}i \)
\( \sqrt{3}i+3+1-\sqrt{3}i \)
の2通りの答えになります。これをそれぞれ計算すると-2と4となります。

答え．
（１）0
（２）\( z = -2，4 \)