この問題のポイント
無理方程式や無理不等式は無理関数のグラフを使って考えよう!
問題の方程式の解は、次の2つのグラフの交点の$x$座標だと考えることができます。
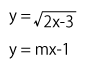
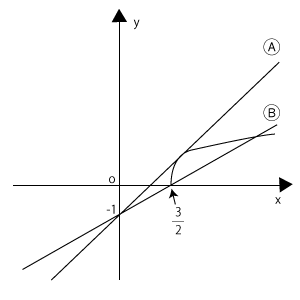
このうち、無理関数のほうをグラフにすると右の図の曲線になります。
そして、\( y = mx-1 \)のグラフは傾きが$m$で切片が-1の直線となります。傾きは$m$という文字なので、いろいろな値をとりますが、\( (0,-1) \)を絶対通るということは確定です。
問題に出ていた無理方程式ですが、その実数解の個数とはこの2つのグラフの交点の個数です。では、どんなときにこの2つのグラフの交点は1個になるでしょう?右の図で直線がⒶの状態になっているときがまず考えられますね。そこから考えてみましょう。
問題に出ていた無理不等式の両辺を2乗すると、
\( 2x-3 = (mx-1)^2 \)
\( 2x-3 = m^2x^2-2mx+1 \)
\( m^2x^2+2(-m-1)x+4 = 0 \)
この方程式の解が1つになるには、この方程式の判別式が= 0にならないといけません。今回は、$x$の係数は2の倍数という形になっていますから、
\( (-m-1)^2-m^2・4 = 0 \)
\( (m+1)^2-m^2・4 = 0 \)
\( m^2+2m+1-4m^2 = 0 \)
\( -3m^2+2m+1 = 0 \)
\( 3m^2-2m-1 = 0 \)
\( (m-1)(3m+1) = 0 \)
直線がⒶの状態になるためには、\( m>0 \)である必要がありますから、解として適切なのは、\( m = 1 \)のほうですね。
つまり、\( m = 1 \)ならば、直線がⒶの状態になり、2つのグラフの交点は1個となります。
ちなみに、\( m = 1 \)なら、問題にあった無理方程式に代入し、解いていくと、\( x = 2 \)となって解が1個になります。
逆に、\( m = 1 \),\( x = 2 \)なら、両辺とも1になり、等式は成立します。
$m$は直線のグラフの傾きなんですから、もし$m$が1より大きくなると、グラフの交点はなくなっちゃいます。そして、1より小さくなると、しばらくは、交点は2個になっていきますね。
交点が2個となるその状態は、直線がⒷの状態になるまで続きます。Ⓑの状態のとき、直線の傾きはどうかを考えましょう。
このときの直線は、図を見てもわかるとおり、点\( \displaystyle \left(\frac{3}{2},0\right) \)を通るときです。ということで、これを\( y = mx-1 \)に代入して、
\( \displaystyle 0 = \frac{3}{2}m-1 \)
これを解くと、\( \displaystyle m = \frac{2}{3} \)
そして、これよりさらに$m$の値を小さくしていくと、2つのグラフの交点の個数は1個だけとなります。
しかし、$m$が0になってしまうと、直線のほうの方程式が\( y = -1 \)となり、$x$軸と平行な直線になってしまうから、2つのグラフが交わることは絶対になくなってしまいます。
さらに、$m$が負の数になってしまっても、2つのグラフは絶対に交わりませんね。
以上のことをまとめると、このような答えになります。
答え.
\( m≦0 \)のとき解なし
\( \displaystyle 0<m<\frac{2}{3} \)のとき1個
\( \displaystyle \frac{2}{3}≦m<1 \)のとき2個
\( m = 1 \)のとき1個
\( m>1 \)のとき解なし