高校数学(3・C)の問題演習
連続関数の決定
※上智大学の入試問題です。
$$
f(x) = \begin{cases}
x^2+1 & (x≦1のとき) \\
-2x^2+ax+b & (x>1のとき)
\end{cases}
$$
で関数$f(x)$を定める。$f(x)$が\( x = 1 \)で微分可能となるような$a$,$b$の値を求めよ。
(半角で入力すること)
回転移動と整数問題
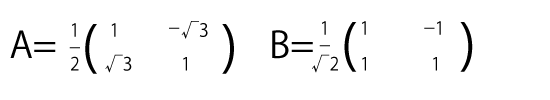
上の行列$A$,$B$で表される1次変換をそれぞれ$f$,$g$とする。変換$f$を$m$回、変換$g$を$n$回適当な順序で行うと、\( P(2,0) \)が\( Q(\sqrt{3},1) \)に移る。$m+n$が最小となるときの$m$,$n$の値をそれぞれ求めなさい。
(半角で入力すること)
面積の2等分
曲線\( y = \sin{x} \)(\( 0≦x≦π \))と$x$軸で囲まれた部分の面積を、次の曲線が二等分するときの$k$の値を求めなさい。
\( \displaystyle y = k\sin{\frac{x}{2}} \)
(解答の際、無理数で答える必要がある場合は、たとえば「ルート3」のときは「√3」(数字は半角)と表記すること。また、数字や符号はすべて半角で入力すること。)
2次曲線の交点
楕円\( x^2+2y^2 = 1 \)と放物線\( 4y = 2x^2+a \) が異なる4つの点で交わるときの$a$の値の範囲を求めなさい。
(解答の際、無理数で答える必要がある場合は、たとえば「ルート3」のときは「√3」(数字は半角)と表記すること。また、数字や符号・不等号はすべて半角で入力すること。)
逆関数と共有点
関数\( f(x) = x^2-2x+k \)(\( x≧1 \))のグラフが、その逆関数\( f^{-1}(x) \)のグラフと異なる2つの共有点をもつときの、$k$の値の範囲を求めなさい。
