問題ページにもどる

この問題のポイント

$A$と$B$の行列はこのように書き換えることができますね。

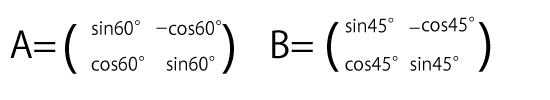
そうです。つまり、行列$A$で表される一次変換（つまり変換$f$）は60°の回転移動、行列$B$で表される一次変換（つまり変換$g$）は45°の回転移動だったというわけです。

ちなみに、座標平面に点$P$，$Q$を置き、そして原点を$O$とすると、$OP$も$OQ$も、距離は2です。ということは、$P$と$Q$は原点$O$を中心とした同じ円の円周上にあります。そして、$∠POQ$は30°になります。

ということは、問題文の言っていたことは、
「点$P$について、60°の回転を$m$回、45°の回転を$n$回やったら、円周上をグルグル回って、30°余分にずれました」
ということと同じだと言えます。

そこで、円周上を$k$回、回ったとすると、この式が成り立つことになりますね。
\( 60°×m+45°×n = 360°×k+30° \)

この式の両辺を15で割って簡単な形にすると、
\( 4m+3n = 24k+2 \)

あとは、この式が成り立つ、$m$と$n$の整数について考えていけばいいことになるのですが、$k$というやっかいな文字ができてしまいました。しかし、考えればいいのは$m+n$が最小のときなので、とりあえず、$k$が0の場合、1の場合と小さい数をあてはめて考えることにしましょう。

［1］\( k = 0 \)の場合

\( 4m+3n = 2 \)
となりますが、これを満たす$m$，$n$は自然数では存在しません。

［2］\( k = 1 \)の場合

\( 4m+3n = 26 \)
となります。これを変形すると、
\( 3n = 26-4m \) …①
そして、$n$は自然数ですから、$3n$は3，6，9，…といったような数になります。3の倍数ですね。そして、それらの倍数は絶対3以上なので、
\( 26-4m≧3 \)

この不等式より、$m$も自然数なので、該当する$m$の値は
\( m = 1，2，3，4，5 \)
それぞれの$m$の値を①の式に代入して、$n$が自然数となるのは、
\( (m,n) = (2,6)，(5,2) \)

このうち、$m+n$が最小となるのは、\( (m,n) = (5,2) \)

［3］\( k≧2 \)の場合

［2］で、\( (m,n) = (5,2) \)、すなわち\( m+n = 7 \)ということが求まりました。$k$が2より大きい場合は、$m+n$は7より大きくなることがわかれば、すなわち、7以下になることがないということがわかれば、晴れて\( (m,n) = (5,2) \)が正解になります。7以下にならないことを証明しましょう。

\( 4m+3n = 24k+2 \)を満たす\( (m,n) \)について、
\( 4(m+n)＞4m+3n≧24・2+2 \)
つまり、$4(m+n)$は50より大きいのですから、$m+n$は12.5より大きいとなり、7を大幅に超えてしまいます。

［1］～［3］より、\( m = 5 \)，\( n = 2 \)とわかりました。

答え．\( m = 5 \)，\( n = 2 \)