高校数学(1・A)の問題演習
内接円と三角比
※2010(平成22)年のセンター試験の問題です。(すべて半角で入力すること)
$△ABC$を\( AB = 3 \),\( BC = 4 \),\( CA = 5 \)である直角三角形とする。
(1)$△ABC$の内接円の中心を$O$とし、円$O$が3辺$BC$,$CA$,$AB$と接する点をそれぞれ$P$,$Q$,$R$とする。このとき、\( OP = OR = \fbox{ア} \)である。
また、\( \displaystyle QR = \frac{\fbox{イ}\sqrt{\fbox{ウ}}}{\fbox{エ}} \)であり、\( \displaystyle \sin∠QPR = \frac{\fbox{オ}\sqrt{\fbox{カ}}}{\fbox{キ}} \)である。
(2)円$O$と線分$AP$との交点のうち$P$と異なる方を$S$とする。このとき、\( AP = \sqrt{\fbox{クケ}} \)であり、\( \displaystyle SP = \frac{\fbox{コ}\sqrt{\fbox{サシ}}}{\fbox{ス}} \)である。
また、点$S$から辺$BC$へ垂線を下ろし、垂線と$BC$との交点を$H$とする。このとき
\( \displaystyle HP = \frac{\fbox{セ}}{\fbox{ソ}} \),\( \displaystyle SH = \frac{\fbox{タ}}{\fbox{チ}} \)
である。したがって、\( \displaystyle \tan∠BCS = \frac{\fbox{ツ}}{\fbox{テ}} \)である。
四分位数と箱ひげ図
※2015(平成27)年のセンター試験の問題です。(すべて半角で入力すること)
ある高校3年生1クラスの生徒40人について、ハンドボール投げの飛距離のデータを取った。次の図1は、このクラスで最初に取ったデータのヒストグラムである。
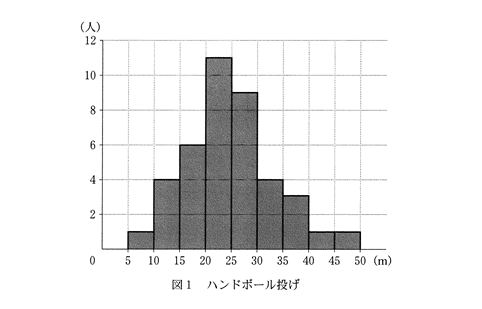
(1)次のアに当てはまるものを、下の[0]~⑧のうちから一つ選べ。
この40人のデータの第3四分位数が含まれる階級は、アである。
[0] 5m以上10m未満
① 10m以上15m未満
② 15m以上20m未満
③ 20m以上25m未満
④ 25m以上30m未満
⑤ 30m以上35m未満
⑥ 35m以上40m未満
⑦ 40m以上45m未満
⑧ 45m以上50m未満
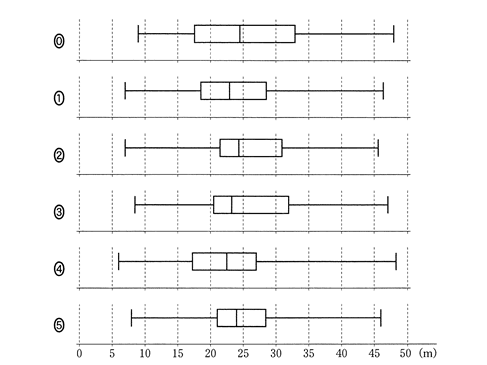
(2)次のイ~オに当てはまるものを、下の[0]~⑤のうちから一つずつ選べ。ただし、イ~オの解答の順序は問わない。
このデータを箱ひげ図にまとめたとき、図1のヒストグラムと矛盾するものは、イ,ウ,エ,オである。
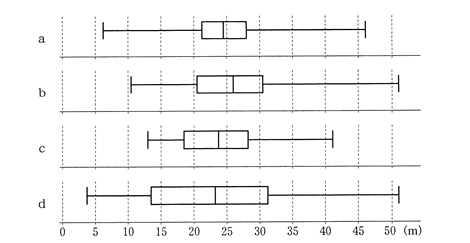
(3)次の文章中のカ,キに入れるものとして最も適当なものを、下の[0]~③のうちから一つずつ選べ。ただし、カ,キの解答の順序は問わない。
後日、このクラスでハンドボール投げの記録を取り直した。次に示したA~Dは、最初に取った記録から今回の記録への変化の分析結果を記述したものである。a~dの各々が今回取り直したデータの箱ひげ図となる場合に、[0]~③の組合せのうち分析結果と箱ひげ図が矛盾するものは、カ,キである。
[0] A―a ① B―b ② C―c ③ D―d
A:どの生徒の記録も下がった。
B:どの生徒の記録も伸びた。
C:最初に取ったデータで上位\( \displaystyle \frac{1}{3} \)に入るすべての生徒の記録が伸びた。
D:最初に取ったデータで上位\( \displaystyle \frac{1}{3} \)に入るすべての生徒の記録は伸び、下位\( \displaystyle \frac{1}{3} \)に入るすべての生徒の記録は下がった。
集合の包含関係
※2018(平成30)年のセンター試験の問題です。(すべて半角で入力すること)
全体集合$U$を$U$ = {$x$|$x$は20以下の自然数}とし、次の部分集合$A$,$B$,$C$を考える。
$A$ = {$x$|\( x \in U \)かつ$x$は20の約数}
$B$ = {$x$|\( x \in U \)かつ$x$は3の倍数}
$C$ = {$x$|\( x \in U \)かつ$x$は偶数}
集合$A$の補集合を\( \overline{A} \)と表し、空集合を∅と表す。
次のキに当てはまるものを、下の[0]~③のうちから一つ選べ。
集合の関係
(a) \( A \subset C \)
(b) \( A \cap B \) = ∅
の正誤の組合せとして正しいものはキである。
[0] |
① |
② |
③ |
|
(a) |
正 |
正 |
誤 |
誤 |
次のクに当てはまるものを、下の[0]~③のうちから一つ選べ。
集合の関係
(c) \( (A \cup C) \cap B \) = {6 , 12 , 18}
(d) \( (\overline{A} \cap C) \cup B = \overline{A} \cap (B \cup C) \)
の正誤の組合せとして正しいものはクである。
[0] |
① |
② |
③ |
|
(c) |
正 |
正 |
誤 |
誤 |
反復試行の確率
※東京理科大学の入試問題を参考に作られています。(すべて半角数字で入力すること)
赤玉1個、白玉2個、黒玉3個が入っている袋がある。この袋から玉を1個取り出し、色を見てからもとの袋へもどす操作を行う。
(a) 操作を3回行うとき、白玉がちょうど2回出る確率は\( \displaystyle \frac{\fbox{ト}}{\fbox{ナ}} \)である。
以下では、操作を$k$回行う。ただし、$k≧2$とする。
(b) 白玉が$(k-1)$回以上出る確率は\( \displaystyle \frac{\fbox{ニ}k+\fbox{ヌ}}{\fbox{ネ}^k} \)である。
(c) 少なくとも2回は黒玉が出る確率は\( \displaystyle \frac{\fbox{ノ}^k-k-\fbox{ハ}}{\fbox{ヒ}^k} \)である。
二次関数の最大・最小
※2013(平成25)年のセンター試験の問題を参考に作られています。(すべて半角で入力すること。区切れ目を・などで区切る必要はありません。)
座標平面上にある点$P$は、点$A(-8,8)$から出発して、直線\( y = -x \)上を$x$座標が1秒あたり2増加するように一定の速さで動く。また、同じ座標平面上にある点$Q$は、点$P$が$A$を出発すると同時に原点$O$から出発して、直線\( y = 10x \)上を$x$座標が1秒あたり1増加するように一定の速さで動く。出発してから$t$秒後の2点$P$,$Q$を考える。点$P$が$O$に到達するのは\( t = \fbox{ア} \)のときである。以下、\( 0<t<\fbox{ア} \)で考える。
点$P$と$x$座標が等しい$x$軸上の点を$P'$,点$Q$と$x$座標が等しい$x$軸上の点を$Q'$とおく。$△OPP'$と$△OQQ'$の面積の和$S$を$t$で表せば
\( S = \fbox{イ}t^2-\fbox{ウエ}t+\fbox{オカ} \)
となる。
これより\( 0<t<\fbox{ア} \)においては、\( \displaystyle t = \frac{\fbox{キ}}{\fbox{ク}} \)で$S$は最小値\( \displaystyle \frac{\fbox{ケコサ}}{\fbox{シ}} \)をとる。
次に、$a$を\( 0<a<\fbox{ア}-1 \)を満たす定数とする。以下、\( a≦t≦a+1 \)における$S$の最小・最大について考える。
(i)$S$が\( \displaystyle t = \frac{\fbox{キ}}{\fbox{ク}} \)で最小となるような$a$の値の範囲は
\( \displaystyle \frac{\fbox{ス}}{\fbox{セ}}≦a≦\frac{\fbox{ソ}}{\fbox{タ}} \)である。
(ii)$S$が$t = a$で最大となるような$a$の値の範囲は\( \displaystyle 0<a≦\frac{\fbox{チ}}{\fbox{ツテ}} \)である。
