この問題のポイント
二次関数で、決められた範囲での最大値と最小値は、頂点の位置が範囲内のどこにあるかで変わる!
点Pは1秒あたり$x$座標が2増加しますが、\( y = -x \)上を動きますから、$y$座標は-2、つまり2ずつ減少していきます。
よって、$t$秒たてば、$x$座標は$2t$増加しますが、$y$座標が$2t$減少しますので、$A(-8,8)$から出発して$t$秒たったときの点$P$の座標は$A(-8+2t,8-2t)$です。
点$P$が$O$に達したということは、$x$座標は0になるはずですから、
\( -8+2t = 0 \)
これを解くと、\( t = 4 \)なので、4秒後に点$P$は$O$に達します。
同じようにして点$Q$を考えると、点$Q$は1秒あたり$x$座標が1増加しますが、\( y = 10x \)上を動きますから、$y$座標は10×1、つまり10ずつ増加していきます。
よって、$t$秒たてば、$x$座標は$t$増加しますが、$y$座標が$10t$増加しますので、原点から出発して$t$秒たったときの点$Q$の座標は$(t,10t)$です。
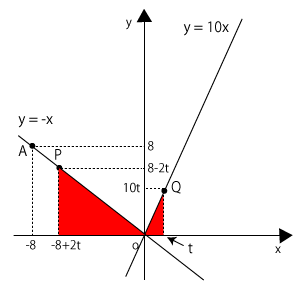
これより、$t$秒後の状況を図にすると、右のようになります。$△OPP'$と$△OQQ'$の面積の和というのは、この図の赤く塗られたところになります。
$△OPP'$の面積を考えると、$P'$の$x$座標は負の数になっているはずなので、
\( OP' = -(-8+2t) = 8-2t \)
よって、$△OPP'$の面積は、
\( \displaystyle \frac{1}{2}×OP'×PP' \)
\( \displaystyle = \frac{1}{2}×(8-2t)×(8-2t) \)
\( \displaystyle = \frac{1}{2}(64-32t+4t^2) \)
\( = 2t^2-16t+32 \)
同じように考えると、$△OQQ'$の面積は、
\( \displaystyle \frac{1}{2}×OQ'×QQ' \)
\( \displaystyle = \frac{1}{2}×t×10t \)
\( = 5t^2 \)
よって、
\( S = 2t^2-16t+32+5t^2 = 7t^2-16t+32 \)
これを平方完成すると、
\( \displaystyle 7\left(t^2-\frac{16}{7}t\right)+32 \)
\( \displaystyle = 7\left(t^2-\frac{16}{7}t+\frac{64}{49}-\frac{64}{49}\right)+32 \)
\( \displaystyle = 7\left(t^2-\frac{16}{7}t+\frac{64}{49}\right)-\frac{64}{7}+32 \)
\( \displaystyle = 7\left(t-\frac{8}{7}\right)^2+\frac{160}{7} \)
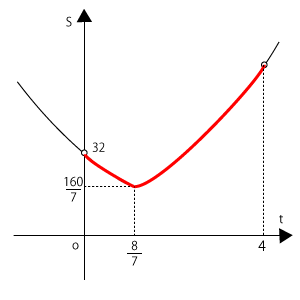
\( 0<t<4 \)での範囲で考えるわけですから、この$S$のグラフをその範囲で書くと右の図の赤線部分ということになります。このグラフより、最小値は放物線の頂点の値とわかります。よって、そのときの$t$の値は\( \displaystyle t = \frac{8}{7} \)
そして、面積の最小値は\( \displaystyle \frac{160}{7} \)
次に、$t$の範囲がどうなるかで最大値・最小値を考える問題が出てきますが、これを考えるときに重要なのは、その範囲内にグラフの頂点があるかや、あるとすれば頂点が範囲内のどこにあるかです。
具体的に言うと、$a$から$b$までの範囲について最大値・最小値を考えるとなったとき、グラフと$a$,$b$の位置関係は次の5パターンになるはずです。
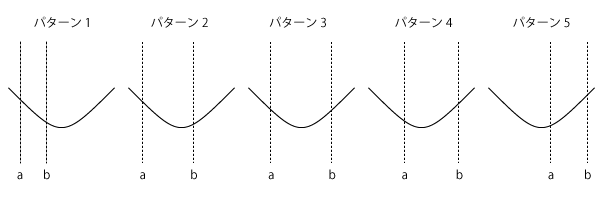
これを念頭に考えていきましょう。
(i)\( \displaystyle t = \frac{8}{7} \)で最小となるということは、頂点で最小値をとるということになります。そうなると、パターン1やパターン5のときは、最小値がグラフの頂点の値にはなりません。よって、$a$から$a+1$の範囲の中に頂点が入っていないといけません。
つまり、\( \displaystyle a≦\frac{8}{7}≦a+1 \)
よって、\( \displaystyle \frac{1}{7}≦a≦\frac{8}{7} \)
(ii)$t = a$で最大となるということは、範囲の左端が最大値をとるということなので、上の図のパターン1とパターン2の場合ですね。また、パターン3の場合だと、範囲の左端と右端が同じ値で最大値をとりますが、問題文では「$t = a$のみで最大」とは書いていませんから、このパターンでもOKですね。
ということは、$a$から$a+1$の範囲の真ん中が頂点になっているか、その真ん中が頂点より左にあるという状態になっていないといけません。$a$と$a+1$の真ん中の$x$座標は、
\( \displaystyle \frac{a+a+1}{2} = a+\frac{1}{2} \)
これが頂点より左にあるということは、頂点の$x$座標より小さくないといけませんので、
\( \displaystyle a+\frac{1}{2}≦\frac{8}{7} \)
これを解くと、\( \displaystyle a≦\frac{9}{14} \)
$a$は\( 0<a<3 \)を満たす定数だったんですから、結局、$a$の範囲は
\( \displaystyle 0<a≦\frac{9}{14} \)
答え.
ア 4
イ 7 ウエ 16 オカ 32
キ 8 ク 7
ケコサ 160 シ 7
ス 1 セ 7 ソ 8 タ 7
チ 9 ツテ 14