この問題のポイント
3辺の長さがa,b,cで面積がSの三角形に内接している円の半径がrのとき、S = r(a+b+c)/2が成り立つ!
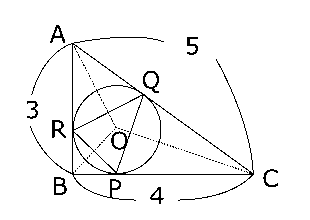
(1)問題文の内容を図にすると右の図のようになります。まず、内接円の半径を求めます。$△ABC$の半径を$r$とすると、
\( △ABC = △OAB+△OBC+△OCA \)
$△ABC$
\( = △OAB+△OBC+△OCA \)
つまり、$△ABC$は、三角形の3辺それぞれを底辺とした三角形を3つたしたものという意味です。そのとき、その3つの三角形それぞれの高さは内接円の半径ということになります。これにより、次の公式が成り立ちなります。
$△ABC$の3辺の長さが$a$,$b$,$c$で面積を$S$、$△ABC$に内接している円の半径を$r$とすると、
\( \displaystyle S = \frac{1}{2}r(a+b+c) \)
この問題では、$△ABC$の面積は、
\( \displaystyle \frac{1}{2}・4・3 = 6 \)
よって、公式を利用すると、
\( \displaystyle 6 = \frac{1}{2}r(3+4+5) \)
\( \displaystyle 6 = \frac{1}{2}・12・r \)
\( 6r = 6 \)
\( ∴r = 1 \)
次に$QR$の長さを考えます。ここで、$△AQR$に着目すると、$∠QAR$は$∠CAB$と同じなんですから、
\( \displaystyle \cos∠QAR = \cos∠CAB = \frac{AB}{CA} = \frac{3}{5} \)
ここで、$AQ$と$AR$の長さがわかれば余弦定理を使って$QR$の長さを求めることができます。ここで、$△ABC$の3辺、つまり$AB$,$BC$,$CA$は内接円$O$の接線になっていますから、
$AR = AQ$,$BR = BP$,$CP = CQ$
よって、\( AR = AQ = α \),\( BR = BP = β \),\( CP = CQ = γ \)とすると、
\( α+β = 3 \),\( β+γ = 4 \),\( γ+α = 5 \)
これを解くと、\( α = 2 \),\( β = 1 \),\( γ = 3 \)
これより、\( AQ = AR = 2 \)とわかりましたから、余弦定理より、
$QR^2$
\( = AQ^2+AR^2-2AQ・AR・\cos∠QAR \)
\( \displaystyle = 2^2+2^2-2・2・2・\frac{3}{5} \)
\( \displaystyle = 4+4-8・\frac{3}{5} \)
\( \displaystyle = \frac{16}{5} \)
\( \displaystyle ∴QR = \frac{4}{\sqrt{5}} \)
つまり、\( \displaystyle QR = \frac{4\sqrt{5}}{5} \)
次に、\( \sin∠QPR \)についてですが、よく見ると、円$O$は$△ABC$の内接円ですが、同時に$△PQR$の外接円になっています。$QR$の長さはちょうど今求めたばかりですが、正弦定理により、
\( \displaystyle \frac{QR}{\sin∠QPR} = 2×(外接円の半径) \)
が成り立ちます。外接円の半径は、ここでは円$O$の半径ですが、それは最初に\( r = 1 \)と求めました。よって、
\( \displaystyle \frac{QR}{\sin∠QPR} = 2 \)
つまり、\( \displaystyle \frac{4\sqrt{5}}{5}÷\sin∠QPR = 2 \)
\( ∴\sin∠QPR \)
\( \displaystyle = \frac{4\sqrt{5}}{5}÷2 \)
\( \displaystyle = \frac{4\sqrt{5}}{5}×\frac{1}{2} \)
\( \displaystyle = \frac{2\sqrt{5}}{5} \)
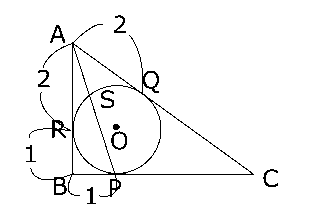
(2)問題文の内容を図にすると右の図のようになります。$AP$についてですが、よく見ると、$△ABP$は直角三角形になっていて、しかも(1)の説明より、\( BP = 1 \),\( AB = 3 \)ということもわかっています。なので、$△ABP$において三平方の定理を使うと、
\( AP^2 = AB^2+BP^2 \)
\( AP^2 = 3^2+1^2 = 9+1 \)
∴\( AP^2 = 10 \)より、\( AP = \sqrt{10} \)です。
次に$SP$についてですが、これについては何かの三角形を利用することはできません。ただし、その$SP$を含む直線$AP$は点$A$を通っていますが、この点$A$については、ほかにも直線$AB$とか直線$AC$も通っています。
そのように考えると、円$O$には直線$AP$と直線$AB$という2本の直線が交わっていることになりますが、このように、1つの円に2本の直線が交わっているときは、方べきの定理を使うことを考えてみましょう。
方べきの定理を利用すると、
\( AS・AP = AR^2 \)
\( AS・\sqrt{10} = 2^2 \)
\( \displaystyle ∴AS = \frac{4}{\sqrt{10}} = \frac{4\sqrt{10}}{10} = \frac{2\sqrt{10}}{5} \)
よって、\( SP = AP-AS \)より、
\( \displaystyle SP = \sqrt{10}-\frac{2\sqrt{10}}{5} = \frac{3\sqrt{10}}{5} \)
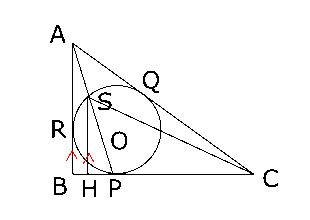
垂線$SH$をひいたのが右の図ですが、$AB$も$SH$も$BC$に対して垂直なので、$AB$//$SH$です。ということは、$△SHP$と$△ABP$は相似ということになりますから、\( HP:BP = SP:AP \)が成り立ちます。
\( \displaystyle ∴HP:1 = \frac{3\sqrt{10}}{5}:\sqrt{10} \)
\( \displaystyle \sqrt{10}HP = \frac{3\sqrt{10}}{5} \)
\( \displaystyle HP = \frac{3\sqrt{10}}{5\sqrt{10}} \)
\( \displaystyle ∴HP = \frac{3}{5} \)
$△SHP$と$△ABP$は相似なので、\( SH:AB = SP:AP \)も成り立つので、
\( \displaystyle SH:3 = \frac{3\sqrt{10}}{5}:\sqrt{10} \)
\( \displaystyle \sqrt{10}SH = \frac{9\sqrt{10}}{5} \)
\( \displaystyle SH = \frac{9\sqrt{10}}{5\sqrt{10}} \)
\( \displaystyle ∴SH = \frac{9}{5} \)
次に、\( \tan∠BCS \)について考えます。\( \displaystyle \tan∠BCS = \frac{SH}{CH} \)(つまり、\( SH÷CH \))です。
\( \displaystyle CH = CP+HP = 3+\frac{3}{5} = \frac{18}{5} \)
よって、\( \displaystyle SH÷CH = \frac{9}{5}÷\frac{18}{5} = \frac{1}{2} \)
\( \displaystyle ∴\tan∠BCS = \frac{1}{2} \)
答え.
ア 1
イ 4 ウ 5 エ 5
オ 2 カ 5 キ 5
クケ 10
コ 3 サシ 10 ス 5
セ 3 ソ 5
タ 9 チ 5
ツ 1 テ 2