高校数学(1・A)の問題演習
三角比を使った二次関数
\( 0°≦θ≦180° \)とする。\( \sin^2θ+\cosθ \)の最大値と最小値を求めなさい。また、そのときの$θ$の値も求めなさい。
(答えは半角で入力し、分数になる場合は、たとえば「3分の1」は「1/3」と記入すること)
式の値(対称式)
※関西大学の入試問題です。
(答えが分数になる場合は、たとえば「5分の2」と入力する場合は、半角で「2/5」と入力すること)
\( x+y = 1 \), \( x^3+y^3 = 3 \)のとき、
(1)\( x^2+y^2 \)の値を求めよ。
(2)\( x^5+y^5 \)の値を求めよ。
チェバの定理
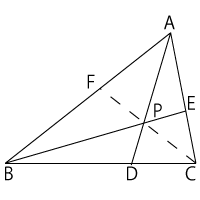
\( AB = 2AC \)の$△ABC$がある。右図のように、$∠A$の二等分線と$BC$の交点を$D$、$CA$を1:2に内分する点を$E$とし、$AD$と$BE$との交点を$P$とする。そして、$CP$と$AB$の交点を$F$とする。このとき、$AF$:$FB$を求めなさい。
(半角で入力すること)
辞書式配列と順列
あ、い、う、え、おの5文字を使って、1番目「あいうえお」、2番目「あいうおえ」、3番目「あいえうお」、…と、国語辞典の見出し語と同じ要領で並べていく。このとき、次の問いに答えなさい。
(1)「うおいあえ」は何番目に来るか、半角で答えなさい。
(2)100番目に来るのはどんな並べ方か答えなさい。
放物線とx軸との共有点と不等式
2次関数 \( y= x^2-2mx−4m+45 \) のグラフが$x$軸と共有点をもたないが、2次関数 \( y= x^2+mx-m+8 \) のグラフが$x$軸と共有点をもつとき、定数$m$の値の範囲を求めなさい。
