この問題のポイント
sinかcosかどちらかに統一した式に変形して考えよう!
sin2θ+cos2θ=1の利用はよく出る!
まず、\( \sin^2θ+\cosθ \)という式は、\( \sin \)も\( \cos \)も両方出てきて考えづらいですから、どちらか1種類に統一しましょう。ここで\( \sin^2θ \)とあるところに注目します。すると、この式が使えることがわかります。
\( \sin^2θ+\cos^2θ = 1 \)
つまり、これを使えば、\( \sin^2θ = 1-\cos^2θ \)となるわけですから、これを代入し、\( \cosθ = t \)とすると
\( 1-\cos^2θ+cosθ \)
\( = -t^2+t+1 \)
これは、2次関数の式になってますね。これの最大値・最小値を考えればいいので、\( y = -t^2+t+1 \)として考えましょう。
まず$t$の範囲を確認しましょう。\( 0°≦θ≦180° \)ですから、\( \cosθ \)の範囲は、
\( -1≦\cosθ≦1 \)
よって、\( -1≦t≦1 \)…①
\( y = -t^2+t+1 \)を平方完成していくと、
$y$
\( = -(t^2-t)+1 \)
\( \displaystyle = -\left(t^2-t+\frac{1}{4}-\frac{1}{4}\right)+1 \)
\( \displaystyle = -\left(t^2-t+\frac{1}{4}\right)+\frac{1}{4}+1 \)
\( \displaystyle = -\left(t-\frac{1}{2}\right)^2+\frac{5}{4} \)
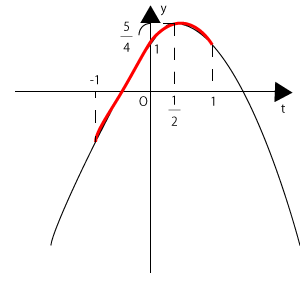
これをグラフにして、①の範囲で考えたのが右図ですね。
赤線の部分が①の範囲の部分ですから、これを見ると、$y$が最大となっているのは、$t$が\( \displaystyle \frac{1}{2} \)のときの値\( \displaystyle \frac{5}{4} \)であるとわかります。
$t$が\( \displaystyle \frac{1}{2} \)ということは、
\( \displaystyle \cosθ = \frac{1}{2} \)、つまり、\( θ = 60° \)です。
一方、$y$が最小となっているのは、
$t$が-1のときの値
\( -(-1)^2-1+1 = -1-1+1 = -1 \)です。
$t$が-1ということですから、
\( \cosθ = -1 \)
つまり、\( θ = 180° \)ですね。
これをまとめると、下のような答えになります。
答え.
\( θ = 60° \)のとき、最大値\( \displaystyle \frac{5}{4} \)
\( θ = 180° \)のとき、最小値-1