この問題のポイント
三角形の三辺上の比がわかっている
→チェバの定理を使おう
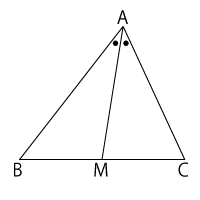
この問題では、角の二等分線がひかれているところがあります。そして、この問題は、比が重要になります。このように、比がからんでいる問題で、二等分線があれば、この定理が使われると、まずは考えましょう。
$△ABC$において、$∠BAC$の二等分線と$BC$の交点を$M$とすると、
\( AB:AC = BM:MC \)
今回の問題では、\( AB = 2AC \)とありましたから、この定理を使うと、
\( BD:DC = AB:AC = 2:1 \)
そして、問題文から、\( CE:EA = 1:2 \)ですね。
ここで、\( BD:DC \)、\( CE:EA \)がわかったわけですね。そして、求めるのは、\( AF:FB \)です。すべて、$BC$、$CA$、$AB$と三角形の三辺上の比ですね。
ここで、今回の問題の図のように、三角形の各頂点と内部の1点を結ぶ直線が、各対辺と交わっていて、なおかつ、三角形の各辺上の比が関係していたら、この定理を思い出してください。
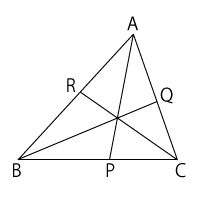
チェバの定理
右図において、
\( \displaystyle \frac{AR}{RB}・\frac{BP}{PC}・\frac{CQ}{QA} = 1 \)
これを問題の図とてらしあわせながらやると、
\( \displaystyle \frac{AF}{FB}・\frac{BD}{DC}・\frac{CE}{EA} = 1 \)
\( \displaystyle \frac{AF}{FB}・\frac{2}{1}・\frac{1}{2} = 1 \)
\( \displaystyle \frac{AF}{FB} = 1 \)
よって、\( AF:FB = 1:1 \)となります。
答え. \( AF:FB = 1:1 \)