高校物理の問題演習
令和6年5月19日
弦の振動と波
※横浜国立大学の入試問題を参考に作られています。
※入力は次の指示にしたがってください。
- 日本語は全角で、それ以外のアルファベットや数字などは半角で入力すること。根号の「ルート」は「ルート」で変換して得られる記号の√、ギリシア文字の「ロー」はρを入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。文字の係数が分数の場合、たとえばaの係数が5分の1ならa/5のように、文字を分子に含める形で入力すること。
- 累乗は、たとえば「aの2乗」ならa^2のように、「○乗」の部分(指数)を^でつないで入力すること。
- 無理数は、たとえば「ルート3」なら√[3]、「ルートa」なら√[a]のように、√の中身を[]で囲って入力すること。
(1)の空欄を埋め、(2),(3)の問いに答えよ。ただし、重力加速度の大きさを$g$とする。
(1) 両端が固定された長さ$l$の弦にできる定常波の腹が$n$個($n$ = 1,2,3,…)のときの波長は (a) と表される。$n$ = 1のときの振動を (b) と呼ぶ。弦を伝わる横波の速さは、張力の大きさ$T$と弦の単位長さあたりの質量(線密度)$ρ$とによって (c) と表される。
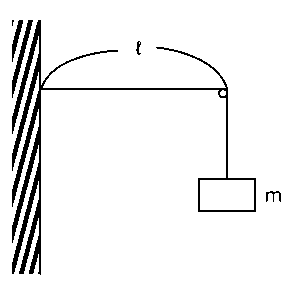
(2) 針金Aを用いて、図のように一端を壁に固定し、他端には滑車を通して質量$m$のおもりを付ける。壁と滑車の間の距離は$l$である。その中央を指ではじくと3個の腹のある定常波ができて、振動数は$f$であった。針金Aの線密度を求めよ。
(3) おもりの質量を変えたら、腹の数が1個になったが、振動数はやはり$f$であった。おもりの質量はいくらか。
令和6年2月18日
くさび形空気層による干渉
※神戸大学の入試問題を参考に作られています。
※入力は次の指示にしたがってください。
- かけ算で使われる×の記号は全角で、それ以外のアルファベットや記号は半角で入力し、ギリシア文字の「ラムダ」はλを入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。文字の係数が分数の場合、たとえばaの係数が5分の1ならa/5のように、文字を分子に含める形で入力すること。
- 累乗は、たとえば「aの2乗」ならa^(2)のように、「○乗」の部分(指数)を^でつなぎ、()で囲って入力すること。
2枚の長方形平板ガラスA,Bを用意する。平板ガラスAには、図1のように表面に深さ$d$の溝が彫られており、溝の方向は平板ガラスAの一つの辺と平行である。溝の深さを測るため、平板ガラスBを、図2のように厚さ$b$の薄いフィルムを間に挟んで重ね、平板ガラスAに対して真上から波長$λ$の光を当てた。平板ガラスAの端からフィルムの先端までの長さを$L$とする。平板ガラスAに対して真上から見たところ、図3のように間隔$a$の干渉
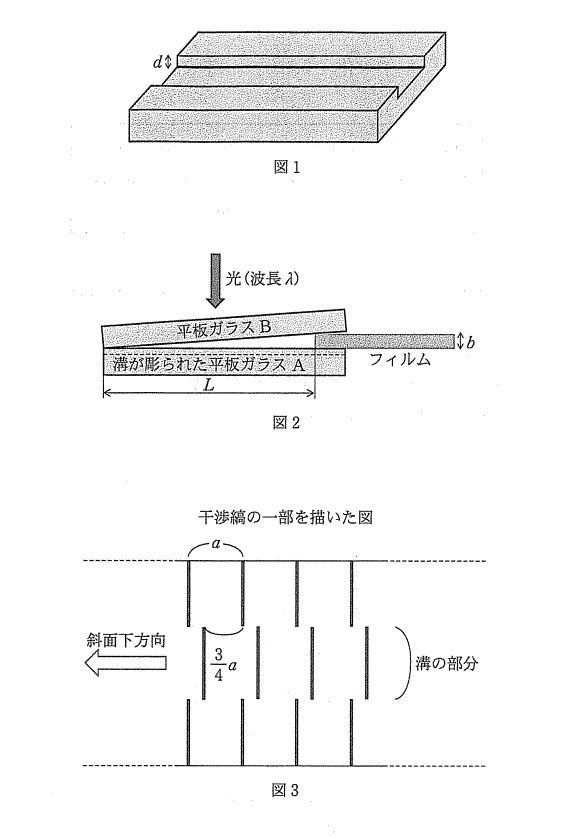
問1 ガラス中での光の速さと波長を求めなさい。
問2 干渉縞の間隔$a$を、$b$,$L$,$λ$のなかから必要なものを用いて表しなさい。
問3 溝の深さ$d$を、$b$,$L$,$λ$,整数$M$($M$ = 0,1,2,…)のなかから必要なものを用いて表しなさい。
問4 2枚の平板ガラスの間を媒質で満たしたとき、干渉縞の間隔が\( \displaystyle \frac{3}{4}a \)になり、干渉縞のずれがなくなった。考え得る溝の深さ$d$を、$b$,$L$,$λ$,整数$N$($N$ = 0,1,2,…)のなかから必要なものを用いて表しなさい。
問5 問4で得られた結果から、\( L = 3.0×10^{-1} \)[m],\( b = 6.0×10^{-5} \)[m],\( a = 1.5×10^{-3} \)[m]とした場合の考え得る溝の深さ$d$のうち、2番目に浅い値を有効数字2桁で求めなさい。
令和5年11月12日
静止摩擦力と動摩擦力
※東京都立大学の入試問題を参考に作られています。
※入力は次の指示にしたがってください。
- 半角で入力すること。ギリシア文字の「ミュー」はμを入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。文字の係数が分数の場合、たとえばaの係数が5分の1ならa/5のように、文字を分子に含める形で入力すること。
- 下付き文字は、たとえば$A_1$ならA1、$B_x$ならBxという要領で入力すること。
- 無理数は、たとえば「ルート3」なら√[3]、「ルートa」なら√[a]のように、√の中身を[]で囲って入力すること。
質量と大きさが等しい均質な三つの直方体形の物体A,B,Cを、図1に示すように端をそろえて積み重ね、水平で滑らかな床の上に置き、中央の物体Bにひもをつけて一定の大きさの力で水平右向きに引っ張る。AとBの間及びBとCの間の摩擦係数は等しいとし、静止摩擦係数を$μ$,動摩擦係数を$μ'$とする。また、Cと床との間に働く摩擦力は無視する。各物体の質量を$m$,重力加速度を$g$として以下の問いに答えよ。
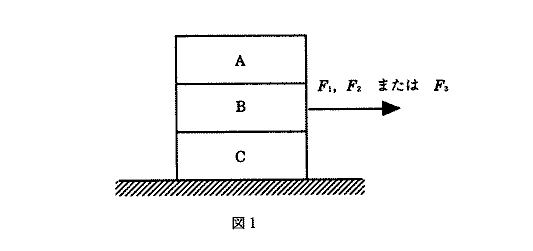
問1 大きさ$F_1$の力で引っ張ったところ、A,B,Cは一体となって運動した。
(1) 物体の加速度の大きさを求めよ。
(2) AとBの間,及びBとCの間に働いている摩擦力の大きさをそれぞれ求めよ。
(3) 静止の状態から水平距離$d$進んだ時点での物体の速さを求めよ。
問2 ある大きさ$F_2$の力で引っ張ったところ、BとCは一体となって運動したがAとBの間では滑り運動が生じた。$F_2$の下限を求めよ。
問3 大きさ$F_3$の力で引っ張ったところ、AとB,BとCの間でそれぞれ滑り運動が生じた。ただし、三つの物体はそれぞれ隣り合う物体と面を接して運動しているとする。A,B,Cのそれぞれの加速度の大きさを求めよ。
令和5年8月10日
光電効果
※名城大学の入試問題です。
※入力は次の指示にしたがってください。
- 半角のみで入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。
- 下付き文字は、たとえば$A_i$ならAi、$B_x$ならBxという要領で入力すること。
光の粒子性を示す現象として、光電効果が知られている。
図1は、光電効果を調べる実験装置の概略図である。図の左方から入射した光は、光電管中の金属板Kに当たり、電子を放出させる。電極Pと金属板Kの間には電位差$V$の電圧がかけられており、放出された電子はPに集まる。PK間の電位差は変化させることができ、その値は電圧計によって測ることができる。このようにして生じた光電流の強さ$I$は、図中の電流計によって測られる。
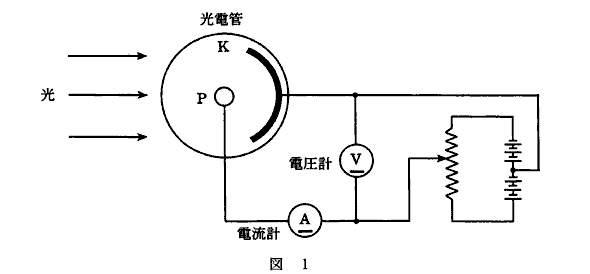
図2は、入射光の強さと振動数を一定にして、電位差$V$を変化させたとき、光電流の強さ$I$が変化する様子を示している。Pの電位を正にして、$V$を大きくしていくと、電流の強さは一定値$I_m$に近づく。逆に、PK間の電位差を$-V_0$にすると光電流は流れなくなる。
図3は、図2の実験における入射光の振動数$ν$を変化させたときの$V_0$の大きさの変化を示している。$ν$が小さくなり、ある値に達すると$V_0$はゼロになる。図中のグラフは$V_0 = aν-b$($a$,$b$は正の定数)という式で表される直線である。
電子の電荷の大きさを$e$として、以下の問に答えよ。
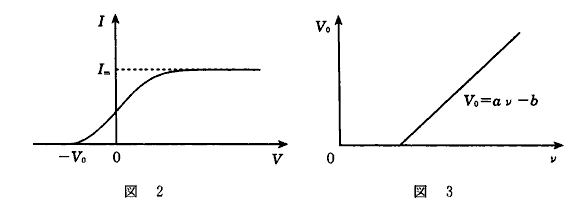
(1) 図2の実験結果から得られる量$I_m$と$V_0$,および$e$のうちのいくつかを用いて次の量を表せ。それぞれの式を記入せよ。
ア 1秒間あたり、放出される電子の個数
イ 放出された電子1個の運動エネルギーの最大値
(2) 図3の実験結果から得られる量$a$と$b$,および$e$のうちのいくつかを用いて次の量を表せ。
ウ 金属板Kの仕事関数
エ プランク定数の値
(3) ある振動数の光を入射させて光電効果を生じさせたとき、その入射光子1個のエネルギーはどれだけか。$I_m$,$V_0$,$a$,$b$および$e$のうちのいくつかを用いて表せ。
令和5年5月7日
万有引力とケプラーの法則
※名古屋大学の入試問題です。
※入力は次の指示にしたがってください。
- 根号をあらわす記号の「ルート」は√で、それ以外はすべて半角で入力すること。
- 無理数は、たとえば「ルート3」なら√3、「ルートa」なら√aのように、√の後にそのまま根号の中身をつづけること。
- 分数は、たとえば3分の1なら[1]/[3]のように、分子と分母をそれぞれ[]で囲って(分子)/(分母)の形で入力すること。
- 下付き文字は、たとえば$a_i$ならai、$b_J$ならbJという要領で入力すること。
- 累乗は、たとえば「aの2乗」ならa^2のように、「○乗」の部分(指数)を^を使って入力すること。
- 文字の係数が分数の場合、たとえばabの係数が5分の2なら[2ab]/[5]のように、分子にすべて含める形で入力すること。
質量$m$の探査機を地球上から打ち上げ、火星表面に着陸させることを考える。以下の問いに答えよ。
(1) はじめに、探査機を地球のまわりで地表すれすれの軌道をまわらせるとしよう。このとき必要な速さ$V_1$を、地表における重力加速度$g$と地球の半径$R$を用いて表せ。
(2) 次に、探査機を加速して、地球の引力を振り切って飛び出させる。探査機がいったん地球の引力を振り切った後は、太陽の引力だけを受けて、地球の公転軌道とまったく同じ軌道を地球と同じ速さでまわる人工惑星になると仮定する。この速さを求めよう。地球の公転軌道は、太陽を中心とした半径$r$の円であると近似する。地球が太陽のまわりを公転する速さ$v_E$を、地球公転軌道の半径$r$と万有引力定数$G$,太陽の質量$M$を用いて表せ。
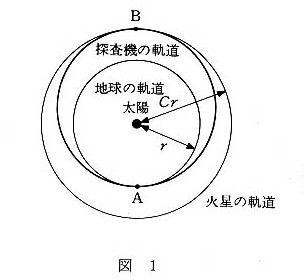
(3) さらに、探査機をごく短い時間だけ加速して、火星に向かう軌道に乗せるとしよう。探査機が描く軌道は、図1のように、太陽を一つの焦点とし、地球の公転軌道に点Aで接し、火星の公転軌道に点Bで接するだ円(楕円)軌道としたい。点Bは太陽をはさんで点Aの反対側の点である。なお、火星の公転軌道は、太陽を中心とした半径$Cr$(地球の公転軌道の半径$r$の$C$倍)の円であると近似する。
(a) ケプラーの第二法則によると、惑星と太陽とをむすぶ線分が一定時間に描く面積は一定である。探査機を楕円軌道を描く惑星とみなしてケプラーの第二法則を用いることによって、点Aで探査機が太陽のまわりを公転する速さ$v_A$と点Bで探査機が太陽のまわりを公転する速さ$v_B$との間の関係を求めよ。
(b) 探査機が点Aでもつべき運動エネルギーを、火星と地球の公転軌道半径の比$C$と探査機の質量$m$,地球の公転速度$v_E$を用いて表せ。
(c) ケプラーの第三法則によると、各惑星の公転周期$T$と軌道の半長軸$a$の間には次の関係が成り立つ:\( T^2 = ka^3 \)($k$は比例定数)。この探査機の軌道の半長軸は線分ABの半分である。探査機が楕円軌道を半周して点Bに達するのは、点Aを出発してから何年後か。$C$を用いて表せ。また、$C$が1.5だとすると、これは何年か、有効数字1桁で答えよ。
