この問題のポイント
円運動については円運動の運動方程式、楕円運動についてはケプラーの第二法則・第三法則を使って考える!
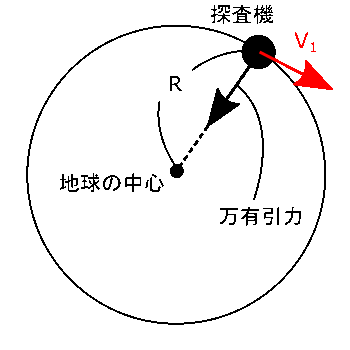
(1) 探査機は地球のまわりで地表すれすれの軌道をまわる運動をするわけなので、右の図のように円運動をすると考えることができます。ということは、探査機は、万有引力を向心力として、速さ$V_1$の等速円運動をすることになります。円運動をする物体については、円運動の運動方程式を使って考えてみましょう。
円運動の半径方向の運動方程式で$F = ma$が成り立ちますが、この問題においての向心力は、地球と探査機の間にはたらく万有引力です。万有引力の大きさは、次のようにあらわせますね?
万有引力の大きさ
万有引力の大きさ$F$は、2つの物体の質量の積に比例し、2つの物体の距離の2乗に反比例する。式にすると、次のとおりとなる。
\( \displaystyle F = G\frac{mM}{r^2} \)
($M$と$m$は物体の質量、$r$は距離、$G$は万有引力定数)
よって、地球の質量を$M_E$とすると、\( \displaystyle ma = G\frac{mM_E}{R^2} \)という運動方程式が成り立ちます。そして、円運動の加速度について、\( \displaystyle a = \frac{V_1^2}{R} \)と書けますから、この2つの式を使って、$a$を消去すると、
\( \displaystyle m・\frac{V_1^2}{R} = G\frac{mM_E}{R^2} \)
\( \displaystyle V_1^2 = \frac{GM_E}{R} \)
\( \displaystyle ∴V_1 = \sqrt{\frac{GM_E}{R}} \) …①
また、地球と物体の間にはたらく万有引力の大きさと、物体の重力の大きさはほぼ等しいので、それを地表すれすれの軌道をまわる探査機にもあてはめると、
\( \displaystyle mg = G\frac{mM_E}{R^2} \)
\( \displaystyle g = \frac{GM_E}{R^2} \)が成り立つので、\( GM_E = gR^2 \)となります。
これを①に代入すると、
\( \displaystyle V_1 = \sqrt{\frac{gR^2}{R}} = \sqrt{gR} \)
(2) 地球の公転軌道とまったく同じ軌道を通るので、太陽を中心とした半径$r$の円運動をすることになります。(1)と同様に円運動の運動方程式を使って考えます。
円運動の半径方向の運動方程式を立てると、\( \displaystyle ma = G\frac{mM}{r^2} \)
加速度について、\( \displaystyle a = \frac{v_E^2}{r} \)と書けるので、$a$を消去すると、
\( \displaystyle m・\frac{v_E^2}{r} = G\frac{mM}{r^2} \)
\( \displaystyle v_E^2 = \frac{GM}{r} \)
よって、\( \displaystyle v_E = \sqrt{\frac{GM}{r}} \)です。
(3)
まず、この問題ではケプラーの法則について触れられているので、それを確認しましょう。天体の運動について、ケプラーは次の共通した法則があることを見出しました。
ケプラーの法則
- 第一法則…
惑星は、太陽を1つの焦点とする楕円上を運動する - 第二法則…
太陽と惑星を結ぶ線分が、一定時間に通過する面積は一定である - 第三法則…
惑星の公転周期$T$の2乗は、軌道の長半径$a$の3乗に比例し、その比例定数はすべての惑星で一定の値となる
(つまり、$T^2 = ka^3$が成り立ち、\( \displaystyle \frac{T^2}{a^3} \)はどの惑星でも同じ値)
天体の運動について軌道が楕円になっているときに、この法則が利用できることが多いです。
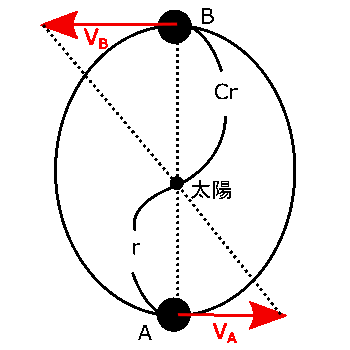
(a) 図1から探査機が進む軌道だけを抜き出すと右の図のようになります。この問題ではケプラーの第二法則を使うことが示されていますが、上の赤枠内にある第二法則の説明について、文章ではイメージがつきづらいと思いますので、右の図を使いながら見てみましょう。
太陽と探査機を結ぶ線分は点線で示されています。探査機や惑星が動くとその線分もあわせて動くことになるので、三角形などの図形ができます。その図形の面積について、時間が同じならば軌道上のどこを動いても同じになるということを意味しているんです。
この問題の場合でいえば、A点からどこまで動くか、B点からどこまで動くかは示されていませんので、速さを矢印であらわしてそれを利用して三角形をつくることにしましょう。すると、図にあるように2つの三角形ができることになります。底辺が$v_A$で高さが$r$の三角形と、底辺が$v_B$で高さが$Cr$の三角形の2つですね?
ケプラーの第二法則より、この2つの三角形の面積は等しいんですから、
\( \displaystyle \frac{1}{2}v_A・r = \frac{1}{2}v_B・Cr \)
\( ∴v_A = Cv_B \)
(b) 探査機が点Aにあるときと点Bにあるときについて、力学的エネルギー保存則より、位置エネルギーと運動エネルギーの和は等しいはずです。探査機には太陽からの万有引力がはたらいていて、万有引力による位置エネルギーは\( \displaystyle -G\frac{mM}{距離} \)とあらわせます。
よって、点Aにおいての位置エネルギーは\( \displaystyle -G\frac{mM}{r} \),探査機の運動エネルギーは\( \displaystyle \frac{1}{2}mv_A^2 \)とおけます。
点Bにおいての位置エネルギーは\( \displaystyle -G\frac{mM}{Cr} \),そこでの探査機の運動エネルギーは\( \displaystyle \frac{1}{2}mv_B^2 \)です。
よって、\( \displaystyle -G\frac{mM}{r}+\frac{1}{2}mv_A^2 = -G\frac{mM}{Cr}+\frac{1}{2}mv_B^2 \)
これに、(a)で求めた\( v_A = Cv_B \)と、(2)で求めた\( \displaystyle v_E = \sqrt{\frac{GM}{r}} \)を変形させてできた式\( GM = rv_E^2 \)を代入して整理すると、
\( \displaystyle \frac{1}{2}mv_A^2-G\frac{mM}{r} = \frac{1}{2}m\left(\frac{v_A}{C}\right)^2-G\frac{mM}{Cr} \)
\( \displaystyle \frac{1}{2}mv_A^2-m\frac{GM}{r} = \frac{1}{2C^2}mv_A^2-\frac{m}{C}・\frac{GM}{r} \)
\( \displaystyle \frac{1}{2}mv_A^2-mv_E^2 = \frac{1}{2C^2}mv_A^2-\frac{m}{C}v_E^2 \)
\( \displaystyle \left(\frac{1}{2}-\frac{1}{2C^2}\right)mv_A^2 = \left(1-\frac{1}{C}\right)mv_E^2 \)
\( \displaystyle \frac{C^2-1}{2C^2}・mv_A^2 = \frac{C-1}{C}・mv_E^2 \)
\( \displaystyle \frac{C^2-1}{2}・mv_A^2 = C(C-1)・mv_E^2 \)
\( \displaystyle \frac{1}{2}mv_A^2 = \frac{C(C-1)}{C^2-1}mv_E^2 \)
因数分解すると、
\( \displaystyle \frac{1}{2}mv_A^2 = \frac{C(C-1)}{(C+1)(C-1)}mv_E^2 \)
$C$はもともと火星の公転軌道の半径が地球のそれの何倍かを示す数値なので、\( C \neq 1 \)より、
\( \displaystyle \frac{1}{2}mv_A^2 = \frac{C}{C+1}mv_E^2 \)
これが点Aにおける運動エネルギーです。
(c) ケプラーの第三法則を利用して考えてみると、地球の公転周期は1年で、その軌道の半長軸は半径の$r$です。一方、探査機の公転周期を$T_1$年とします。軌道の半長軸(ABの半分)は(a)の解説にある図を使って考えると\( \displaystyle \frac{r+Cr}{2} \)です。
よって、
\( \displaystyle \frac{1^2}{r^3} = \frac{T_1^2}{\left(\displaystyle\frac{r+Cr}{2}\right)^3} \)
\( \displaystyle \frac{1^2}{r^3} = \frac{T_1^2}{r^3・\left(\displaystyle\frac{1+C}{2}\right)^3} \)
\( \displaystyle \frac{T_1^2}{\left(\displaystyle\frac{1+C}{2}\right)^3} = 1 \)
\( \displaystyle T_1^2 = \left(\frac{1+C}{2}\right)^3 \)
\( \displaystyle ∴T_1 = \left(\frac{1+C}{2}\right)^{\frac{3}{2}} \)
AからBまで移動するのは軌道を半周することと同じですから、点Bに達するのは、点Aを出発してから\( \displaystyle \frac{1}{2}\left(\frac{1+C}{2}\right)^{\frac{3}{2}} \)年後ですね。
そして、$C = 1.5$のとき、
\( \displaystyle \frac{1}{2}\left(\frac{1+1.5}{2}\right)^{\frac{3}{2}} = 0.69… \)
小数第2位を四捨五入すると、0.7と求まります。
答え.
(1)
\( \displaystyle V_1 = \sqrt{gR} \)
(2)
\( \displaystyle v_E = \sqrt{\frac{GM}{r}} \)
(3)
(a)
\( v_A = Cv_B \)
(b)
\( \displaystyle \frac{C}{C+1}mv_E^2 \)
(c)
\( \displaystyle \frac{1}{2}\left(\frac{1+C}{2}\right)^{\frac{3}{2}} \)年後
$C = 1.5$のとき、0.7年後