この問題のポイント
干渉縞は空気層が等しいところにできる!
くさび形空気層では空気層の厚さの2倍の経路差があり、位相も変わるので、明線や暗線ができる条件に注意!
問1 ガラス中の光の速さを$c'$,波長を$λ'$とします。屈折の法則より、
\( c'・n = c・1.0 \)なので、\( \displaystyle c' = \frac{c}{n} \)
\( λ'・n = λ・1.0 \)なので、\( \displaystyle λ' = \frac{λ}{n} \)
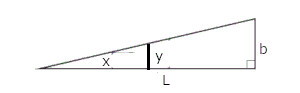
問2 この問題では干渉縞の暗線が現れていますが、この暗線は、上にあるガラスBの下面で反射した光と下にあるガラスAの上面で反射した光が干渉してできたものです。その2つの光について考えます。右の図のように、ガラスA,Bの交点から$x$離れたところにあるとし、そこでの空気層の厚さを$y$とします。
2つの反射光のうち、下にあるガラスAの上面で反射した光だけ、空気層の中を往復しているので、2つの光の経路差は、空気層の厚さの往復分である$2y$だけあります。
そして、上にあるガラスBで反射した光は自由端反射(屈折率の大きい物質から小さい物質に入るときに起こる反射)で位相は変化しませんが、下にあるガラスAで反射した光は固定端反射(屈折率の小さい物質から大きい物質に入るときに起こる反射)で位相が逆になります。
つまり、2つの光は互いに逆位相となるので、暗線ができる条件は、経路差が半波長の偶数倍と等しくなるときということになります。
つまり、\( \displaystyle 2y = \frac{λ}{2}・2m \)($m$ = 0,1,2,…)
\( \displaystyle y = \frac{1}{2}mλ \)($m$ = 0,1,2,…)…①で暗線ができることになります。
ここで、問題文にあるとおり、フィルムの厚さが$b$,ガラスAの端からフィルムの先端までの長さが$L$なので、三角形の相似の関係より、
\( x:y = L:b \)が成り立ちます。
これを変形すると、\( Ly = bx \)より、\( \displaystyle y = \frac{bx}{L} \)
これを①に代入すると、\( \displaystyle \frac{bx}{L} = \frac{1}{2}mλ \)
\( 2bx = mλL \)
\( \displaystyle x = \frac{mλL}{2b} \)($m$ = 0,1,2,…)
求める間隔$a$とは、\( \varDelta x \)のことなので、\( \displaystyle \frac{λL}{2b} \)ということになります。
問3 溝があるところでは、溝の深さの分だけ、空気層が厚くなり、厚さのずれが生じてしまいます。干渉縞は空気層が等しいところにできるので、溝があるところだけは、その分だけ斜面下方向にずれて空気層が等しいところに縞ができるようになっているわけですね。
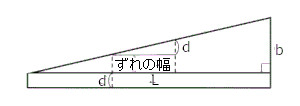
溝があるところとないところで経路差が等しい暗線の関係をあらわしたのが右の図です。この図にある「ずれの幅」がどれほどかを考えることが、この問題を解くカギとなります。問題文には斜面下方向に\( \displaystyle \frac{3}{4}a \)ずれたことが書かれていますが、これがそのまま「ずれの幅」になるとは限りません。
溝のない部分での暗線の間隔は$a$ですが、溝がどれだけ深いかがわかりませんから、\( \displaystyle \frac{3}{4}a \)よりさらに$a$1個分多くずれている可能性もありますし、$a$2個分多くずれている可能性もあります。問題で与えられた干渉縞の図だけではそれが判断できませんから、結局「ずれの幅」は\( \displaystyle \frac{3}{4}a+Ma \)とおくしかありません。
「ずれの幅」がわかりましたから、さっきの問2と同じように、三角形の相似の関係を利用すると、
\( \displaystyle \left(\frac{3}{4}a+Ma\right):d = L:b \)
\( \displaystyle \left(\frac{3}{4}+M\right)a:d = L:b \)
\( \displaystyle Ld = \left(\frac{3}{4}+M\right)ab \)
\( \displaystyle d = \left(\frac{3}{4}+M\right)\frac{ab}{L} \)
さっきの問2で\( \displaystyle a = \frac{λL}{2b} \)と求めましたので、それを代入すると、
\( \displaystyle d = \left(\frac{3}{4}+M\right)・\frac{λL}{2b}・\frac{b}{L} \)
\( \displaystyle = \left(\frac{3}{4}+M\right)\frac{λ}{2} \)
問4 溝による干渉縞のずれがなくなり、干渉縞の間隔は\( \displaystyle \frac{3}{4}a \)になったということは、同じ経路差の暗線が\( \displaystyle \frac{3}{4}a \)ずれたらいいということになります。ただし、さっきの問3と同じように、どれだけの間隔の分だけ動けばいいかはわかりませんから、$m$を自然数とおくと、\( \displaystyle \frac{3}{4}a \)の$m$倍だけ動いたと考える必要があります。
なので、問3と同じように考えれば、
\( \displaystyle d = \frac{3}{4}ma・\frac{ab}{L} \)
問2で求めた\( \displaystyle a = \frac{λL}{2b} \)を代入すると、
\( \displaystyle d = \frac{3}{4}m・\frac{λL}{2b}・\frac{b}{L} = \frac{3}{8}mλ \)
そして、さっきの問3で\( \displaystyle d = \left(\frac{3}{4}+M\right)\frac{λ}{2} \)と求めたのですから、
\( \displaystyle \left(\frac{3}{4}+M\right)\frac{λ}{2} = \frac{3}{8}mλ \)
\( \displaystyle \frac{3}{8}λ+\frac{M}{2}λ = \frac{3}{8}mλ \)
\( 3+4M = 3m \)
\( 4M = 3(m-1) \)
4と3は互いに素ですから、この式が成り立つには、$M$は3の倍数でなければいけません。よって、$M = 3N$として、これを\( \displaystyle d = \left(\frac{3}{4}+M\right)\frac{λ}{2} \)に代入すると、
\( \displaystyle d = \left(\frac{3}{4}+3N\right)\frac{λ}{2} \)
\( \displaystyle = \left(\frac{1}{4}+N\right)\frac{3λ}{2} \)
問5 さっきの問4では\( \displaystyle d = \left(\frac{1}{4}+N\right)\frac{3λ}{2} \)と求まりましたが、$λ$の値が与えられるかわりに、$a$や$b$の値が与えられています。よって、$λ$を$a$や$b$が使われた形であらわす必要があります。
\( \displaystyle a = \frac{λL}{2b} \)と問2で求めていましたから、これを使うと、
\( λL = 2ab \)
\( \displaystyle λ = \frac{2ab}{L} \)
これを\( \displaystyle d = \left(\frac{1}{4}+N\right)\frac{3λ}{2} \)に代入すると、
\( \displaystyle d = \left(\frac{1}{4}+N\right)・\frac{3}{2}・\frac{2ab}{L} \)
\( \displaystyle = \left(\frac{1}{4}+N\right)\frac{3ab}{L} \)
2番目に浅い値を求めるので、$N$ = 0,1,2,…とあるうち$N = 1$と与えられた数値を代入しましょう。
\( \displaystyle d = \left(\frac{1}{4}+1\right)・\frac{3・1.5×10^{-3}・6.0×10^{-5}}{3.0×10^{-1}} \)
\( ≒ 1.1×10^{-6} \)[m]
答え.
問1 光の速さ…\( \displaystyle \frac{c}{n} \),波長…\( \displaystyle \frac{λ}{n} \)
問2 \( \displaystyle a = \frac{λL}{2b} \)
問3 \( \displaystyle d = \left(\frac{3}{4}+M\right)\frac{λ}{2} \)
問4 \( \displaystyle d = \left(\frac{1}{4}+N\right)\frac{3λ}{2} \)
問5 \( d = 1.1×10^{-6} \)[m]