問題ページにもどる

この問題のポイント

解説に入る前に、この問題では物体を引っ張ることによって摩擦力が働いていることに気づきましたでしょうか？そして、どの向きに摩擦力が働くかをおさえていますでしょうか？この問題では下の図に示された形で摩擦力が働いていますね。

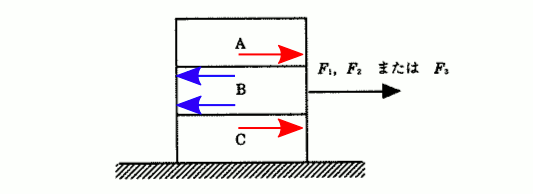
物体Bを引っ張るわけなので、物体Bには右向きの力が働きます。摩擦力は運動を妨げる向きに働きますから、物体Bは、物体A・Cから図の青の矢印の向きに摩擦力を受けます。

しかし、物体Aと物体Cは、物体Bから図の赤の矢印の向きに摩擦力を受けます。2つの物体間には同じ大きさで逆向きの力が働くという作用反作用の法則があるので、青の矢印の向きと反対方向の力が働いているためです。物体Aと物体Cも右向きに動きますが、摩擦力も右向きになるのはこのためです。

これを前提に解説を進めます。物体Aと物体Bの間に働く摩擦力を$f_x$，物体Bと物体Cの間に働く摩擦力を$f_y$とします。

問1

(1)　求める加速度を$a_1$とします。物体の加速度と力の関係は\( ma = F \)という運動方程式で表せますから、ここで3つの物体それぞれの運動方程式をたてます。

物体Aについては、\( ma_1 = f_x \)　…[a]
物体Bについては、摩擦力が働いているので、\( ma_1 = F_1-f_x-f_y \)　…[b]
物体Cについては、\( ma_1 = f_y \)　…[c]

この3つの方程式すべてをたすと、\( 3ma_1 = F_1 \)
\( \displaystyle ∴a_1 = \frac{F_1}{3m} \)

(2)　AとBの間に働く摩擦力は$f_x$でした。さっきの(1)で求めたものを、[a]に代入すると、
\( \displaystyle f_x = m・\frac{F_1}{3m} = \frac{F_1}{3} \)

BとCの間に働く摩擦力は$f_y$でした。同様に考えて、[c]に代入すると、
\( \displaystyle f_y = m・\frac{F_1}{3m} = \frac{F_1}{3} \)

(3)　この問題では物体の速さを求めなければいけません。そして、進んだ距離が$d$として与えられていますから、速さと距離が使われている公式である\( v^2-v_0^2 = 2ax \)を使うことを考えてみましょう。

引っ張らないとA，B，Cは動かなかったんですから、初速度は0です。よって、求める物体の速さを$v$として公式にあてはめると、
\( \displaystyle v^2-0^2 = 2・\frac{F_1}{3m}・d \)
\( \displaystyle v^2 = \frac{2F_1d}{3m} \)
\( v＞0 \)より、\( \displaystyle v = \sqrt{\frac{2F_1d}{3m}} \)

問2

静止している物体が動き出さないように働く力を静止摩擦力といいます。AやCはひもを引っ張ってもBに対してずっと静止した状態でしたので、問1で考えた摩擦力はすべて静止摩擦力です。物体が静止したままならば、物体に加える力が大きくなればなるほど、静止摩擦力も大きくなっていきます。

でも、どんな物体でもじゅうぶん大きな力を加えると動き出しますから、静止摩擦力の大きさには限界があります。この限界の静止摩擦力を超えると物体は動き出すわけですが、静止摩擦力の限界値を最大静止摩擦力または最大摩擦力といいます。これについては、求める公式があります。

問題文で「下限を求めよ」と限界値にふれていることと、BとCは一体となって運動したままということから、$F_2$はAにとって最大摩擦力以上の力であり、そのせいで静止していたAが滑り出した（＝動き出した）と考えられます。

この最大摩擦力を考えるために、物体Aにかかる垂直抗力を求めると、物体Aにかかる重力と同じはずなので$mg$とおくことができます。なので、物体Aの最大摩擦力は$μmg$です。

よって、3つの物体の加速度を$a_2$とすると、さっきの問1と同じようにこのような運動方程式をたてることができます。

物体Aについては、\( ma_2 = μmg \)　…[d]
物体Bについては、\( ma_2 = F_2-μmg-f_y \)
物体Cについては、\( ma_2 = f_y \)
（物体BとCについては滑り運動は起きていませんから、$f_y$は最大摩擦力になっていないことに注意！）

この3つの方程式をたすと、\( 3ma_2 = F_2 \)　…[e]
$a_2$は問題を解くうえで勝手においた文字なのでこれを消す必要がありますが、[d]より、\( a_2 = μg \)
これを[e]に代入すると、\( F_2 = 3μmg \)

問3

動き出した後に物体に働く摩擦力を動摩擦力といいます。この問題では、AとB，BとCの間両方とも滑り運動が生じたので、物体どうしが動いていることになります。よって、摩擦力としては動摩擦力を考えることになるわけですが、動摩擦力は次の公式で求まります。

これをもとに、まずAとBの間に働いた動摩擦力を考えましょう。さっきの問2で考えたとおり、物体Aにかかる垂直抗力は$mg$ですから、AとBの間に働いた動摩擦力は公式より、$μ'mg$です。

一方、BとCの間に働いた動摩擦力はどうでしょうか？物体Cには物体A・Bの2つの重力がかかります。ということは、物体Cが受ける重力は$2mg$ですから、物体Cが物体Bに対して与える垂直抗力は$2mg$です。よって、BとCの間に働いた動摩擦力は$2μ'mg$だとわかります。

あとは、A，B，Cのそれぞれの加速度を$α$，$β$，$γ$とおけば、さっきの問1や問2と同じように運動方程式をたてることができます。

物体Aについては、\( mα = μ'mg \)　…[f]
物体Bについては、\( mβ = F_3-μ'mg-2μ'mg \)　…[g]
物体Cについては、\( mγ = 2μ'mg \)　…[h]
とおけます。

よって、[f]より、Aの加速度は\( α = μ'g \)
[g]は\( mβ = F_3-3μ'mg \)となるので、Bの加速度は\( \displaystyle β = \frac{F_3}{m}-3μ'g \)
[h]より、Cの加速度は\( γ = 2μ'g \)

答え．
問1
(1)
\( \displaystyle \frac{F_1}{3m} \)
(2)
AとBの間…\( \displaystyle \frac{F_1}{3} \)
BとCの間…\( \displaystyle \frac{F_1}{3} \)
(3)
\( \displaystyle \sqrt{\frac{2F_1d}{3m}} \)
問2
$3μmg$
問3
Aの加速度…$μ'g$
Bの加速度…\( \displaystyle \frac{F_3}{m}-3μ'g \)
Cの加速度…$2μ'g$

©All Rights Reserved