高校物理の問題演習
令和5年1月29日
気体の分子運動論
※九州工業大学の入試問題を参考に作られています。
※入力は次の指示にしたがってください。
- かけ算で使われる×の記号のみ全角で、それ以外はすべて半角で入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。
- 下付き文字は、たとえば$A_i$ならAi、$b_x$ならbxという要領で入力すること。
- 累乗は、たとえば「aの2乗」ならa^2のように、「○乗」の部分(指数)を^を使って入力すること。
- 問題文中にある\( \overline{v^2} \)、\( \overline{v_x^2} \)を入力する場合はそれぞれ、v^2-,vx^2-と入力すること。
図1のように1辺の長さが$L$の立方体容器に閉じ込めた$n$モルの単原子分子の理想気体を考える。容器の体積は変わらない。アボガドロ定数を$N_0$とすると、分子数は$N = nN_0$となる。分子数$N$はきわめて大きく、分子は容器内で特定の方向にかたよることなく運動している。ただし、分子同士の衝突は考えなくてよいものとする。容器の壁と分子との衝突は弾性衝突である。壁の$x$軸に垂直な面のうち、$x = L$にある面を壁$S_x$とする。
分子1個の質量を$m$,分子の速さを$v$,気体の圧力を$p$,気体の体積を$V$(=$L^3$),気体の絶対温度を$T$,気体定数を$R$とする。以下の問いに答えよ。
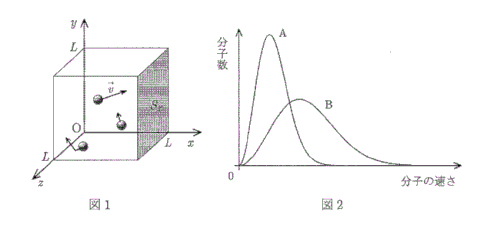
[1] 最初に、1個の分子が容器の壁$S_x$と衝突する場合を考える。衝突前の分子の速度の$x$成分,$y$成分,$z$成分を、それぞれ$v_x$,$v_y$,$v_z$とする。
(1) 1回の衝突で分子が壁$S_x$に及ぼす力積を$m$と$v_x$を用いて表せ。
(2) 分子が壁$S_x$と衝突してから再び$S_x$に衝突するまでの時間を、$L$と$v_x$を用いて表せ。
(3) 時間$t$の間に、分子が壁$S_x$と衝突する回数を$L$,$t$,$v_x$を用いて表せ。
(4) 時間$t$の間に、壁$S_x$が受ける力積を$L$,$m$,$t$,$v_x$を用いて表せ。
(5) 壁$S_x$が受ける平均の力$f$を$L$,$m$,$v_x$を用いて表せ。
[2] 次に、$N$個の分子が容器の壁$S_x$と衝突することを考える。分子の速さの2乗$v^2$と速度の$x$成分の2乗$v_x^2$の$N$個についての平均をそれぞれ\( \overline{v^2} \),\( \overline{v_x^2} \)とする。
(6) \( \overline{v^2} \)と\( \overline{v_x^2} \)の関係を等式で表せ。
(7) 壁$S_x$が$N$個の分子から受ける力$F$を、$L$,$N$,$m$,\( \overline{v^2} \)を用いて表せ。
(8) 壁$S_x$の受ける圧力$p$を、$N$,$V$,$m$,\( \overline{v^2} \)を用いて表せ。
(9) $N$個の分子が持つ運動エネルギーを、$N_0$,$N$,$R$,$T$を用いて表せ。
(10) 実験を行い測定したところ、気体の温度が\( 3.00×10^2 \)Kであるとき、分子1個の運動エネルギーの平均は\( 6.21×10^{-21} \)Jであった。ボルツマン定数\( k = R/N_0 \)[J/K]を有効数字3桁の数字で答えよ。
[3] 容器の気体の温度が絶対温度$T_A$のときを状態A,絶対温度$T_B$のときを状態Bとする。図2の曲線A,Bは、それぞれの状態での分子の速さの分布である。
(11) $T_A$と$T_B$の関係を表すのは次の(a)~(c)のうちのどれか。(半角のアルファベット小文字のみを入力すること)
{(a) \( T_A>T_B \),(b) \( T_A = T_B \),(c) \( T_A<T_B \)}
令和4年10月23日
比熱と熱容量
※南山大学の入試問題です。(答えはすべて全角カタカナのみで入力すること)
\( 4.00×10^2 \)Wのヒーターを内蔵した容器がある。ヒーターのスイッチが入っていない状態で、容器に\( 1.50×10^2 \)gの氷を入れると容器と氷は一様に-10.0℃となった。ヒーターのスイッチを入れると、全体の温度は図のように時間の経過とともに変化した。ヒーターのスイッチを入れてから184s後に、全体の温度は30.0℃となり、ヒーターのスイッチを切った。このことから氷の融解熱は (10) J/gとわかる。また、容器の熱容量は (11) J/Kで、氷の比熱は (12) J/(g・K)となる。ここで、質量\( 1.35×10^2 \)gで85.0℃の金属球を容器に入れて、十分な時間が経った後、全体の温度を測ったところ35.0℃になった。この金属球の比熱は (13) J/(g・K)である。ただし、容器と外部との熱の出入りがなく、ヒーターの熱容量は無視できるものとする。また、水の比熱は4.20J/(g・K)とする。
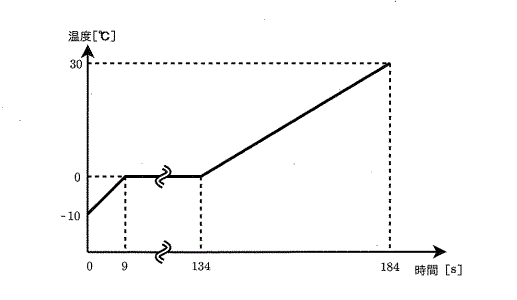
(10)の選択肢
㋐ \( 2.40×10 \) ㋑ \( 1.33×10^2 \)
㋒ \( 3.33×10^2 \)
㋓ \( 3.57×10^2 \)
㋔ \( 4.67×10^2 \)
(11)の選択肢
㋐ \( 3.67×10 \) ㋑ \( 6.67×10^2 \)
㋒ \( 1.21×10^3 \)
㋓ \( 1.84×10^3 \)
㋔ \( 6.37×10^3 \)
(12)の選択肢
㋐ \( 8.00×10^{-1} \) ㋑ 2.16
㋒ 2.40
㋓ \( 3.23×10^2 \)
㋔ \( 3.60×10^2 \)
(13)の選択肢
㋐ \( 3.71×10^{-1} \) ㋑ \( 3.92×10^{-1} \)
㋒ \( 4.67×10^{-1} \)
㋓ \( 4.94×10^{-1} \)
㋔ \( 7.78×10^{-1} \)
令和4年7月31日
点電荷による電場・電位
※千葉大学の入試問題です。
※入力は次の指示にしたがってください。
- 日本語の文字は全角で、それ以外は半角で入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。文字の係数が分数の場合、たとえばaの係数が5分の3なら3a/5のように、分子のところに文字を含めること。
- 無理数は、たとえば「ルート3」なら√[3]のように、√の中身を[]で囲って入力すること。
- 下付き文字は、たとえば$A_i$ならAi、$B_x$ならBxという要領で入力すること。
- 累乗は、たとえば「aの2乗」ならa^2のように、「○乗」の部分(指数)を^を使って入力すること。
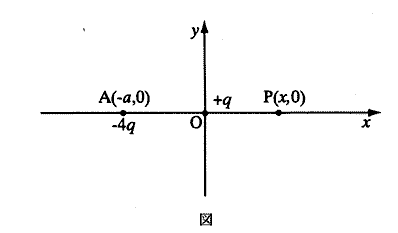
図のように、$xy$面上の原点$O$と点\( A(-a,0) \)($a>0$とする)に、それぞれ$+q$と$-4q$($q>0$)の点電荷を固定する。以下の問に答えなさい。クーロンの法則の比例係数を$k_0$とし、電位の基準点は無限遠にとるものとする。また、重力の影響は考えなくてよい。
問1 $x$軸上の点\( P(x,0) \)の電場の$x$成分と$y$成分を、それぞれ座標$x$の関数として求めなさい。ただし$x>0$とする。
問2 点\( P(x,0) \)の電位を座標$x$の関数として求めなさい。ただし$x>0$とする。
問3 $xy$面上の電位0の等電位線を表す方程式を求め、どんな図形か説明しなさい。
図中の2つの点電荷から$+x$方向に十分離れた$x$軸上の点$R$に、大きさが$q$で符号のわからない点電荷$Q$(質量$m$)を静かにおいたところ、原点に近づく方向に動き始めた。
問4 点電荷$Q$の符号は正負どちらか。
問5 点電荷$Q$はどこまで原点$O$に近づくか、最も近づいたときの点電荷$Q$と原点$O$の距離を求めなさい。
問6 点電荷$Q$が動き始めてから原点$O$に最も近づくまでの間の、速さの最大値はいくらか。
令和4年5月1日
気柱の共鳴
※佐賀大学の入試問題を参考に作られています。(半角のみで入力し、分数を入力したい場合は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること)
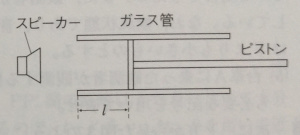
気柱の共鳴について考える。図のように、空気中に置かれたガラス管に右側からピストンを挿入し、左側に発生音の振動数を調節できるスピーカーを置いた。音の速さ$V$は一定であり、開口端補正はないものとする。次の問いに答えよ。
最初にピストンを固定した。このときの、ガラス管の左の管口からピストンの左端までの距離を$l$とする。スピーカーの振動数を0からゆっくりと増していった。
(1)最初の共鳴が起こる振動数を$l$と$V$を用いて表せ。
(2)$n$回目($n$ = 2,3,…)の共鳴が起こるときに気柱にできる定在波(定常波)の節の数を$n$を用いて表せ。
(3)$n$回目の共鳴が起こるときの定在波の波長を$n$と$l$を用いて表せ。
(4)$n$回目の共鳴が起こるときの振動数を$n$,$l$,$V$を用いて表せ。
次に、スピーカーの振動数を(4)の$n = 2$の値に固定して、ピストンをガラス管の左の管口の位置からゆっくりと右に動かした。
(5)最初の共鳴が起こったときの、管口からピストン左端までの距離を$l$を用いて表せ。
さらに、ピストンを(5)の位置に固定したまま、スピーカーの振動数をゆっくりと大きくした。
(6)次に共鳴が起こる振動数の値を$l$と$V$を用いて表せ。
令和4年1月9日
運動量と力積
※( )内の年度の大学入学共通テスト・センター試験の問題です。(答えはすべて半角数字で入力すること)
次の問いA(問1),B(問2),C(問3・問4)に答えよ。
A Aさんは固定した台座の上に立っていて、Bさんは水平な氷上に静止したそりの上に立っている。図1のように、Aさんが質量$m$のボールを速さ$v_A$,水平面となす角$θ_A$で斜め上方に投げたとき、ボールは速さ$v_B$,水平面となす角$θ_B$で、Bさんに届いた。そりとBさんを合わせた質量は$M$であった。ただし、そりと氷との間に摩擦力ははたらかないものとする。空気抵抗は無視できるものとし、重力加速度の大きさを$g$とする。
(2021(令和3))
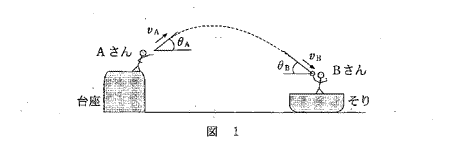
問1 Bさんが届いたボールを捕球して、そりとBさんとボールが一体となって氷上をすべり出す場合を考える。捕球した後、そりとBさんの速さが一定値$V$になった。$V$を表す式として正しいものを、次の①~④のうちから一つ選べ。$V$ = 1
① \( \displaystyle \frac{(m+M)v_B\cos{θ_B}}{M} \)
② \( \displaystyle \frac{(m+M)v_B\sin{θ_B}}{M} \)
③ \( \displaystyle \frac{mv_B\cos{θ_B}}{m+M} \)
④ \( \displaystyle \frac{mv_B\sin{θ_B}}{m+M} \)
B 次の問いに答えよ。
(2018(平成30))
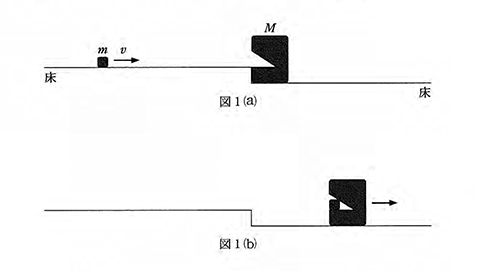
問2 図1(a)のように、速さ$v$で進む質量$m$の小物体が、質量$M$の静止していた物体と衝突し、図1(b)のように二つの物体は一体となり動き始めた。一体となった物体の運動エネルギーとして正しいものを、下の①~⑨のうちから一つ選べ。ただし、床は水平でなめらかであるとする。
① \( \displaystyle \frac{Mv^2}{2} \) ② \( \displaystyle \frac{mv^2}{2} \)
③ \( \displaystyle \frac{(M+m)v^2}{2} \)
④ \( \displaystyle \frac{M^2v^2}{2(M+m)} \)
⑤ \( \displaystyle \frac{m^2v^2}{2(M+m)} \) ⑥ \( \displaystyle \frac{Mmv^2}{2(M+m)} \)
⑦ \( \displaystyle \frac{M^2v^2}{M+m} \) ⑧ \( \displaystyle \frac{m^2v^2}{M+m} \)
⑨ \( \displaystyle \frac{Mmv^2}{M+m} \)
C 氷の上で石を滑らせることについて考えよう。はじめ、図1のように、質量$M$の人が質量$m$の石とともに、速度$V_0$で摩擦のない水平な氷の上を滑っている。ただし、すべての運動は一直線上で起こるとし、図1・図2の右向きを正の向きとする。
(2000(平成12))
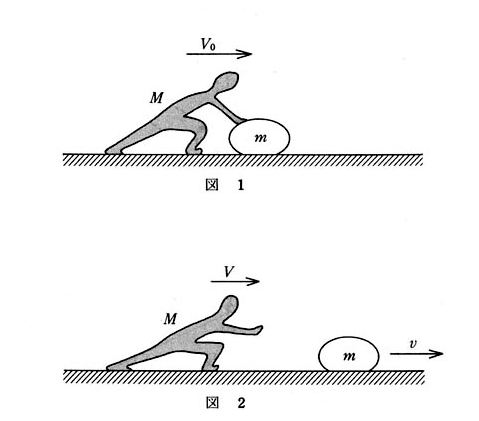
問3 人が一定の力$F$を時間\( \varDelta t \)の間だけ加えて石を水平に押したところ、図2のように、人と石は互いに離れて、人の速度は$V$,石の速度は$v$となった。$V$と$v$はそれぞれいくらか。正しいものを、次の①~⑤のうちから一つずつ選べ。
$V$ = 2
$v$ = 3
① $V_0$ ② \( \displaystyle V_0+\frac{F}{m}\varDelta t \)
③ \( \displaystyle V_0-\frac{F}{m}\varDelta t \)
④ \( \displaystyle V_0+\frac{F}{M}\varDelta t \)
⑤ \( \displaystyle V_0-\frac{F}{M}\varDelta t \)
問4 問3で石が人の手を離れたとき、人がちょうど静止した。この場合、人と石の運動エネルギーの合計は、石を押した後には、押す前に比べて何倍になったか。正しいものを、次の①~④のうちから一つ選べ。 4 倍
① \( \displaystyle \frac{M+m}{m} \) ② \( \displaystyle \frac{M+m}{M} \)
③ \( \displaystyle \frac{m}{M+m} \) ④ \( \displaystyle \frac{M}{M+m} \)
