この問題のポイント
電場とは電荷が受ける静電気力で、電位とは電荷がもつ位置エネルギー!
山にたとえて概念を理解し、クーロンの法則との関係で公式を理解する!
この問題では電場や電位が主になっていますが、電場や電位を考えるうえで重要な法則としてクーロンの法則というものがあります。まず、この法則を見てみましょう。
$q_1$[C],$q_2$[C]の2つの電荷が$r$[m]離れて置かれているとする。このとき、2つの電荷の間にはたらく静電気力を$F$[N]とすると、
\( \displaystyle F = k\frac{q_1q_2}{r^2} \)
(つまり、静電気力は距離の2乗に反比例し、電気量の積に比例する)
$k$はクーロン定数といい、$9.0×10^9$[Nm2/C2]をあらわす
これをもとにすると電場の公式がわかりやすくなります。ちなみに電場とは+1Cの電荷が受ける静電気力のことをいいます。問題を解きつつ確認していきましょう。
問1 この問題では電場を考えますが、電場や電位は山や谷で考えるとわかりやすいのですが(+の電気なら山の頂上に電荷が、-の電気なら谷底に電荷があると考える)、転がったりするとどれほどの力を与えるかを示すものにあたるので、山や谷にたとえると傾斜の傾きにあたります。
その電場については、次の公式で考えることができます。
$q$[C]の点電荷から受ける電場を考える。クーロンの法則より
\( \displaystyle F = k\frac{q×1}{r^2} = k\frac{q}{r^2} \)
よって、$q$[C]の点電荷から$r$[m]離れたところが受ける電場を$E$とすると、
\( \displaystyle E = k\frac{q}{r^2} \)
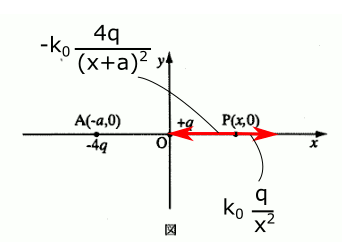
点$P$に+1Cの電荷をおいたとして、原点と点$A$からその電荷にかかる力の合成は右の図のような関係になります。ここで、電場の$x$成分を$E_x$,$y$成分を$E_y$とします。
$x$成分については、原点からの電場は\( \displaystyle k_0\frac{q}{x^2} \),点$A$からの電場は\( \displaystyle \left\{-k_0\frac{4q}{(x+a)^2}\right\} \)なので、
\( \displaystyle E_x = k_0\frac{q}{x^2}+\left\{-k_0\frac{4q}{(x+a)^2}\right\} \)
\( \displaystyle = \frac{k_0q}{x^2}-\frac{4k_0q}{(x+a)^2} \)
\( \displaystyle = \frac{(x+a)^2k_0q-4x^2k_0q}{x^2(x+a)^2} \)
\( \displaystyle = \frac{x^2k_0q+2axk_0q+a^2k_0q-4x^2k_0q}{x^2(x+a)^2} \)
\( \displaystyle = \frac{-3x^2k_0q+2axk_0q+a^2k_0q}{x^2(x+a)^2} \)
\( \displaystyle = \frac{k_0q(-3x^2+2ax+a^2)}{x^2(x+a)^2} \)
\( \displaystyle = -\frac{k_0q(x-a)(3x+a)}{x^2(x+a)^2} \)
そして、$y$成分である$E_y$については0です。
問2 この問題では電位を考えますが、電位とは+1Cの電荷を置いたときの位置エネルギーのことをいいます。山や谷にたとえると、まさに電荷が置かれた場所の高さにあたります。
電位については、次の公式で考えることができます。
$q$[C]の点電荷から$r$[m]離れたところにおける電位を$V$とすると、
\( \displaystyle V = k\frac{q}{r} \)
ここで、電場は静電気力、つまり力なので方向をもったベクトル量であるのに対して、電位は位置エネルギーで方向がないのでスカラー量をあらわしています。よって、この問題では、原点と点$A$それぞれの点電荷による電位のスカラー和を考えればいいことになります。
原点からの電位は\( \displaystyle k_0\frac{q}{x} \),点$A$からの電位は\( \displaystyle k_0\frac{-4q}{x+a} \)より、求める電位は、
\( \displaystyle k_0\frac{q}{x}+k_0\frac{-4q}{x+a} \)
\( \displaystyle = \frac{k_0q(x+a)-4k_0qx}{x(x+a)} \)
\( \displaystyle = \frac{k_0qx+ak_0q-4k_0qx}{x(x+a)} \)
\( \displaystyle = \frac{-3k_0qx+ak_0q}{x(x+a)} \)
\( \displaystyle = -\frac{k_0q(3x-a)}{x(x+a)} \)
問3 任意の点\( (x,y) \)における電位を$V_A$とすると、
\( \displaystyle V_A = k_0\frac{q}{\sqrt{x^2+y^2}}+k_0\frac{-4q}{\sqrt{x^2+y^2}} \)
これの$V_A = 0$の等電位線を考えるわけなので、
\( \displaystyle k_0\frac{q}{\sqrt{x^2+y^2}}+k_0\frac{-4q}{\sqrt{x^2+y^2}} = 0 \)
の式について考えればよいですね?
この式を整理すると、
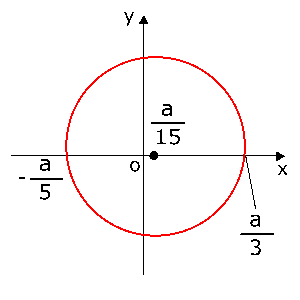
\( \displaystyle \left(x-\frac{a}{15}\right)^2+y^2 = \left(\frac{4}{15}a\right)^2 \)
となります。これは図のように、中心\( \displaystyle \left(\frac{a}{15},0\right) \),半径\( \displaystyle \frac{4}{15}a \)の円をあらわします。
問4 問1で求めた$E_x$,$E_y$について、$E_x<0$,$E_y = 0$とわかりました。$x$軸方向正の向きに十分離れた点$R$について、このことから、電場は$x$軸方向負の向きということがわかります。
点電荷$Q$はその電場の向きに動いたのですから、これより符号は正(+)とわかります。
問5 点$R$における電荷$Q$の静電気力による位置エネルギーは0で、静かに電荷を置いたわけですから運動エネルギーも0です。よって、点\( (x,0) \)における$Q$の速さを$v$とすると、エネルギー保存則より、次の方程式が成り立つことになります。
\( \displaystyle \frac{1}{2}mv^2-\frac{k_0q^2(3x-a)}{x(x+a)} = 0 \)
原点$O$に最も近づいたときには止まっているはずなので、速さは0となるわけですから、$v = 0$を代入して、
\( \displaystyle -\frac{k_0q^2(3x-a)}{x(x+a)} = 0 \)
$a>0$ですから、この方程式が成り立つには$3x-a = 0$、すなわち\( \displaystyle x = \frac{a}{3} \)となればいいですね。
問6 点電荷の電位について、次の関係が成り立ちます。
$q$[C]の点電荷から$r$[m]離れた点$A$における電位を$V$とすると、点$A$から無限遠の点まで+1Cの電荷を運ぶときに静電気力がする仕事と等しく、それは次の式で求められる。
\( \displaystyle \int_r^\infty k\frac{q}{x^2}dx = k\frac{q}{r} \)
そして、ある点に置いた+1Cの電荷が別の点まで移動したとき、電場の大きさは(2点間の電位差)÷(2点間の距離)に等しく、電場の方向は電位が減少する向きである。
このことより、電場が0のときに電位は極値をとるといえます。そこで問1で求めた関数を使って、
\( \displaystyle -\frac{k_0q(x-a)(3x+a)}{x^2(x+a)^2} = 0 \)
\( x \neq 0 \)ですから、\( (x-a)(3x+a) = 0 \)
よって、\( \displaystyle x = a,-\frac{a}{3} \)ですが、$x>0$なので、$x = a$です。
つまり、原点$O$に近づくとき、$x = a$の点にて、$E_x<0$から$E_x>0$に変わるので、電位(位置エネルギー)は極小値をとることとなります。求める速さを$v_a$とすると、エネルギー保存則より、
\( \displaystyle \frac{1}{2}mv_a^2 = \frac{k_0q^2(3a-a)}{a(a+a)} \)
これを解くと、\( \displaystyle v_a = q\sqrt{\frac{2k_0}{ma}} \)
答え.
問1 $x$成分…\( \displaystyle -\frac{k_0q(x-a)(3x+a)}{x^2(x+a)^2} \) $y$成分…0
問2 \( \displaystyle -\frac{k_0q(3x-a)}{x(x+a)} \)
問3 方程式は\( \displaystyle \left(x-\frac{a}{15}\right)^2+y^2 = \left(\frac{4}{15}a\right)^2 \)より、中心\( \displaystyle \left(\frac{a}{15},0\right) \),半径\( \displaystyle \frac{4}{15}a \)の円をあらわす
問4 正
問5 \( \displaystyle \frac{a}{3} \)
問6 \( \displaystyle q\sqrt{\frac{2k_0}{ma}} \)