この問題のポイント
気柱の中に波4分の1個分がいくつ含まれているかに注目し、そこから波長や振動数、気柱の長さなどを考えて行く!
(1)気柱内では空気が振動することで音が発生します。気柱内の振動のしかたに合った空気を送りこむことで音が鳴り、この現象を共鳴とよぶわけです。ふつう、空気の振動は縦波(進行方向と同じ向きに振動する波)ですが、気柱の問題では横波として波の形を描いて考えることができます。
この問題のように、片方が閉じている気柱を閉管といいますが、閉管の閉じているほうでは空気が振動できず、開いているほうは空気は振動できますから、閉じているほうは節になり、開いているほうは腹になります。

すると、最初の共鳴としての波は一番簡単な形になるはずなので、右の図aのような波になるはずです。波の\( \displaystyle \frac{1}{4} \)個分になっていますね?この振動を基本振動といいます。この図を見るとわかるとおり、$l$は波の\( \displaystyle \frac{1}{4} \)個分と等しいので、\( \displaystyle l = \frac{λ}{4} \)といえます。
この問題では振動数を波の速さと管の長さで表すわけですが、振動数と速さについて\( v = fλ \)、つまり波の振動数と波長をかけると波の速さになるという公式がありますから、これを利用してみましょう。
スピーカーから出る音の速さは$V$で一定なので、\( V = fλ \)
そして、\( \displaystyle l = \frac{λ}{4} \)でしたから、\( 4l = λ \)
よって、\( V = f・4l \)より、\( \displaystyle f = \frac{V}{4l} \)
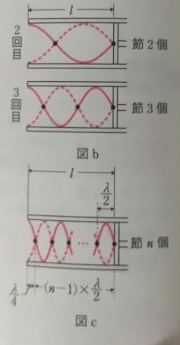
(2)閉管の閉じているところは節になるので、それを考えて2回目、3回目の共鳴の波を描くと右の図bのようになります。2回目の波では節が2個、3回目の波では節が3個あります。このことから、共鳴の回数と節の数は一致するとわかるので、$n$回目の共鳴における波の節の数は$n$個です。
ちなみに、2回目の共鳴では、波の\( \displaystyle \frac{1}{4} \)個分の長さが3つ含まれています。よって、このときの振動を3倍振動といいます。また、3回目の共鳴では、波の\( \displaystyle \frac{1}{4} \)個分の長さが5つ含まれていますから、このときの振動を5倍振動といいます。
(3)$n$回目の共鳴の波を描くと図cのようになります。節は$n$個あるので、隣り合う節と節の距離は$(n-1)$個分あります。また、管口の腹から最初の節までの部分もあるので、気柱の長さ$l$は図cのとおり、管口の腹から最初の節までの部分と隣り合う節と節の距離$(n-1)$個分の合計といえます。
管口の腹から最初の節までの部分では、波の\( \displaystyle \frac{1}{4} \)個分の波長になっていて、節と節の間ではそれぞれ波の\( \displaystyle \frac{1}{4} \)個分の長さが2つ、つまり\( \displaystyle \frac{1}{2} \)個分の波長になっています。よって、求める波長を$λ_n$とすると、
\( \displaystyle l = \frac{λ_n}{4}+(n-1)×\frac{λ_n}{2} \)
\( \displaystyle l = \frac{λ_n}{4}+\frac{λ_n}{2}n-\frac{λ_n}{2} \)
\( \displaystyle l = \frac{λ_n}{2}n-\frac{λ_n}{4} \)
\( \displaystyle l = \frac{λ_n}{4}(2n-1) \)
\( (2n-1)λ_n = 4l \)
\( \displaystyle λ_n = \frac{4l}{2n-1} \)
(4)振動数を求める問題なので、(1)と同じように\( v = fλ \)を使って求めることを考えてみましょう。
ここでもスピーカーから出る音の速さは$V$のはずです。そして、波長は(3)で求めたとおりなので、求める振動数を$f_n$とすると、
\( \displaystyle V = f_n・\frac{4l}{2n-1} \)より、\( \displaystyle f_n = \frac{(2n-1)V}{4l} \)
(5)$n = 2$のときの共鳴で振動数を固定するわけですから、そのときの音波の波長は(3)で求めた式より、
\( \displaystyle λ_2 = \frac{4l}{2・2-1} = \frac{4}{3}l \)です。
この音波を使って、(1)のようにまた最初の共鳴を考えるわけですから、その最初に起こる共鳴は図aのような基本振動のときでしょう。このときの気柱の長さと波長の\( \displaystyle \frac{1}{4} \)個分は等しかったはずです。つまり、求める気柱の長さは、$λ_2$の\( \displaystyle \frac{1}{4} \)と等しいので、
\( \displaystyle \frac{λ_2}{4} = \frac{1}{4}×\frac{4}{3}l = \frac{l}{3} \)
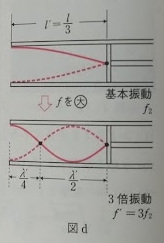
(6)最初の共鳴が起こった状態で、またピストンを固定し、そして振動数を変えて共鳴を起こしたということは、実質2回目の共鳴を起こしたのと同じ状態になっています。ということは、(2)で考えた2回目の共鳴と同じ状態とみなせるわけなので、図dで示しているように3倍振動となっているはずです。
これより、波の\( \displaystyle \frac{1}{4} \)個分の長さが3つ含まれていることになります。ただし、この問題で求めるのは振動数なので、(5)で求めた最初の共鳴のときの振動数を求めておきましょう。(4)で求めた式を利用すると、最初の共鳴のときの振動数は
\( \displaystyle \frac{(2・2-1)V}{4l} = \frac{3V}{4l} \)
図dで示しているように、波の\( \displaystyle \frac{1}{4} \)個分の長さが3つ含まれている3倍振動となっているわけなので、求める振動数はこれの3倍ですから、
\( \displaystyle 3×\frac{3V}{4l} = \frac{9V}{4l} \)
答え.
(1)\( \displaystyle \frac{V}{4l} \) (2)$n$
(3)\( \displaystyle \frac{4l}{2n-1} \) (4)\( \displaystyle \frac{(2n-1)V}{4l} \)
(5)\( \displaystyle \frac{l}{3} \) (6)\( \displaystyle \frac{9V}{4l} \)