高校物理の問題演習
令和3年10月3日
力のつりあい
※( )内の年度の大学入学共通テスト・センター試験の問題です。(答えはすべて半角数字で入力すること)
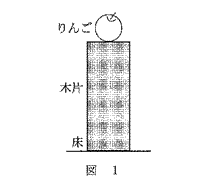
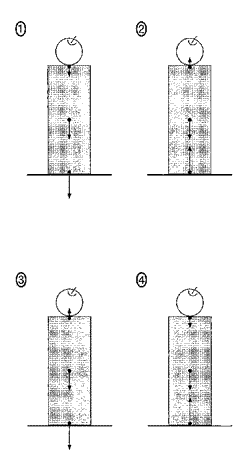
問1 図1のように、床の上に直方体の木片が置かれ、その木片の上にりんごが置かれている。木片には、地球からの重力,床からの力,りんごからの力がはたらいている。木片にはたらくすべての力を表す図として最も適当なものを、次の①~④のうちから一つ選べ。
(2021(令和3))
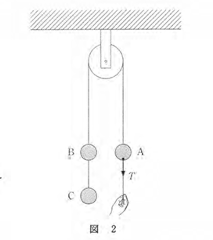
問2 図2のように、3個の物体A,B,Cを静止させた。物体の質量はいずれも$m$である。このとき、物体Aを鉛直下向きに引くひもの張力の大きさ$T$として正しいものを、下の①~⑦のうちから一つ選べ。
(2018(平成30))
① \( \displaystyle \frac{1}{3}mg \) ② \( \displaystyle \frac{1}{2}mg \) ③ \( \displaystyle \frac{2}{3}mg \)
④ $mg$ ⑤ \( \displaystyle \frac{4}{3}mg \) ⑥ \( \displaystyle \frac{3}{2}mg \)
⑦ $3mg$
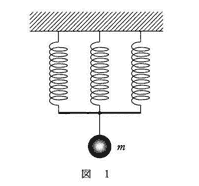
問3 図1のように、自然の長さが同じでばね定数が$k$の3本の軽いばねを水平な天井に等間隔に固定し、ばねの下端に軽い棒を水平に取り付けた。この棒の中央から質量$m$の物体を軽い糸でつるすと、3本のばねはそれぞれ自然の長さから$l$だけ伸びて静止した。伸び$l$を表す式として正しいものを、下の①~⑤のうちから一つ選べ。ただし、3本のばねは同一鉛直面内にあり、棒は変形しないものとし、重力加速度の大きさを$g$とする。$l$ = 1
(2020(令和2))
① \( \displaystyle \frac{mg}{3k} \) ② \( \displaystyle \frac{mg}{2k} \) ③ \( \displaystyle \frac{mg}{k} \)
④ \( \displaystyle \frac{2mg}{k} \) ⑤ \( \displaystyle \frac{3mg}{k} \)
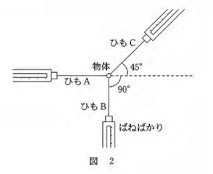
問4 図2のように、物体に3本のひもをつなぎ、ばねばかりで水平面内の3方向に引き、静止させた。このとき、ひもA,B,Cから物体にはたらく力の大きさをそれぞれ$F_A$,$F_B$,$F_C$とする。これらの比として正しいものを、下の①~⑥のうちから一つ選べ。$F_A$:$F_B$:$F_C$ = 2
(2018(平成30))
① $1$:$1$:$1$ ② $1$:$1$:\( \sqrt{2} \)
③ $1$:$2$:\( \sqrt{2} \)
④ $1$:$1$:$2$
⑤ \( \sqrt{2} \):\( \sqrt{2} \):$1$ ⑥ \( \sqrt{2} \):$2$:$1$
令和3年6月27日
交流回路の基本事項
※浜松医科大学の入試問題です。
※入力は次の指示にしたがってください。
- 日本語の文字は全角で、それ以外は半角で入力すること。円周率$π$は「パイ」、ギリシア文字のωは「オメガ」、θは「シータ」で変換して出るものを入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。分数の前にマイナスの記号をつけるときは、たとえば-2/5のように、分子のところに半角の-を入力すること。
- 文字の係数が分数の場合、たとえばaの係数が5分の3なら3a/5のように、分子のところに文字を含めること。
- 無理数は、たとえば「ルート3」なら√[3]のように、√の中身を[]で囲って入力すること。
- 下付き文字は、たとえば$A_i$ならAi、$B_x$ならBxという要領で入力すること。
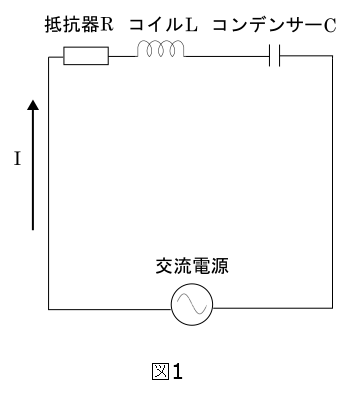
図1のように抵抗値$R$の抵抗器、自己インダクタンス$L$のコイル、電気容量$C$のコンデンサーを直列に接続した回路に、角周波数$ω$の交流電源を接続し、交流電圧$V$を加えた。
時刻$t$において、回路を流れる電流は、図1の矢印の向きを正として、\( I = I_0\sin{ωt} \)であった。このとき、抵抗器、コイル、コンデンサーにかかる電圧の瞬時値(瞬間値)はそれぞれ$V_R$,$V_L$,$V_C$であった。電源電圧$V$の位相は、回路を流れる電流$I$の位相よりも、$θ$だけ進んでいた。円周率を$π$とする。以下の問いに答えよ。
なお、必要ならば次の公式を用いてもよい。
\( A\sin{x}+B\cos{x} = \sqrt{A^2+B^2}\sin{(x+α)} \),ただし\( \displaystyle \tanα = \frac{B}{A} \)
1.電流の実効値$I_e$を求めよ。
2.$V_R$,$V_L$,$V_C$をそれぞれ求め、時刻$t$の関数で示せ。
3.\( \cosθ \)の値を、$I_0$,$R$,$ω$,$L$,$C$のうち必要なものを用いて表せ。
4.$V$の最大値$V_0$および実効値$V_e$を求め、$I_0$,$R$,$ω$,$L$,$C$を用いて表せ。
5.この回路のインピーダンス$Z$を、$R$,\( \cosθ \)を用いて表せ。
6.回路に加える交流電源の周波数をゆっくりと変化させたところ、特定の周波数で大きな電流が流れた。この現象のことを何というか、答えよ。また、最大電流が流れたときの周波数$f_0$を求めよ。
令和3年3月21日
レンズによる像
※名古屋大学の入試問題です。(答えはすべて半角で入力すること)
凸レンズを使って、虫めがねから顕微鏡の原理を考えてみる。なお、以下の設問において、レンズの厚みは無視できるものとする。
(1) 焦点距離$OF_1$ = $OF_2$ = 20mmの凸レンズがある。物体$AA'$をレンズの中心$O$より24mm左側の位置においてみると、レンズの右側に拡大された倒立像ができる。倒立像$BB'$と凸レンズとの距離$OB$,および拡大率を求めよ。
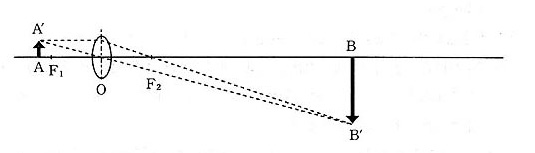
虫めがねで物体を拡大して観察する場合を考える。物体$AA'$を凸レンズの焦点よりわずかにレンズに近い位置においてみる。すると、レンズの右側に像はつくられないが、右側の焦点の付近からレンズをのぞくと、拡大された正立虚像$BB'$が見えることになる。
(2) 明視の距離(虚像と目との距離)を250mmとした場合について、レンズと物体$AA'$との距離$OA$を求めよ。さらにそのときの拡大率を求めよ。なお、目の位置はレンズの焦点$F_2$とする。
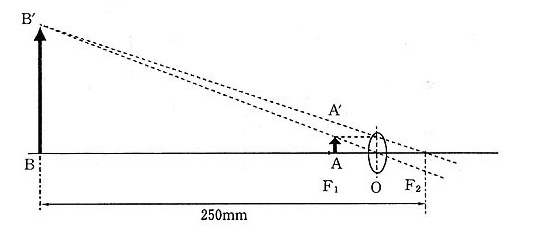
2枚の凸レンズを組み合わせて顕微鏡を作成する。レンズ$L1$の焦点距離は20mm,レンズ$L2$の焦点距離は50mmである。物体$AA'$とレンズ$L1$の距離を24mmとする。
(3) 図のように、レンズ$L2$の右側の焦点の位置からのぞき、明視の距離(虚像$CC'$と目との距離)が250mmであった場合、$L1$と$L2$の間隔はいくらか。
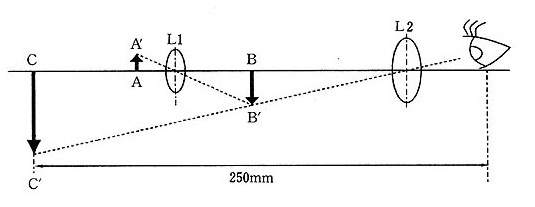
(4) 目で見るのではなく、スクリーン上に像$CC'$を結像させる。スクリーンは、レンズ$L2$から右側に300mm離れた場所に設置する。そのとき、設問(3)の状態において$L1$と$L2$の間隔を変えないとすると、物体$AA'$とレンズ$L1$との距離をいくらずらせばよいか。また、そのときの総合倍率($CC'/AA'$)はいくらか。(物体をレンズから遠ざける場合は負の数で、レンズに近づける場合は正の数で入力すること)
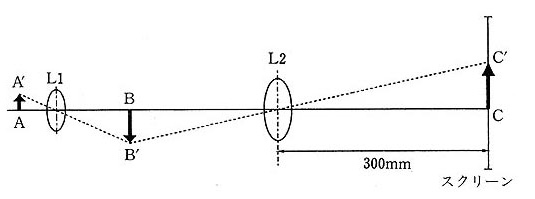
(5) 物体$AA'$,レンズ$L2$,スクリーンの位置は変えずに、レンズ$L1$を焦点距離が30mmのレンズに交換し、スクリーンに像を結像させたい。レンズ$L1$による倍率が1倍以上である場合のレンズ$L1$とレンズ$L2$の間隔はいくらになるか。また、このときの総合倍率を求めよ。
令和2年12月6日
箔検電器と静電誘導
※2009(平成21)年のセンター試験の問題です。(答えはすべて半角数字で入力すること)
図1のような装置は
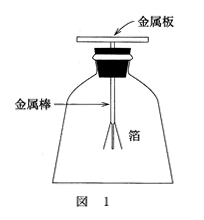
問1 箔検電器の動作を説明する次の文章の空欄 ア ~ ウ に入れる記述a~cの組合せとして最も適当なものを、下の①~⑥のうちから一つ選べ。
帯電していない箔検電器の金属板に正の帯電体を近づけると、 ア ため自由電子が引き寄せられる。その結果、金属板は負に帯電する。一方、箔検電器内では イ ため帯電体から遠い箔の部分は自由電子が減少して正に帯電する。帯電した箔は、 ウ ため開く。
a 同種の電荷は互いに反発しあう
b 異種の電荷は互いに引き合う
c 電気量の総量は一定である
ア |
イ |
ウ |
|
① |
a |
b |
c |
② |
a |
c |
b |
③ |
b |
a |
c |
④ |
b |
c |
a |
⑤ |
c |
a |
b |
⑥ |
c |
b |
a |
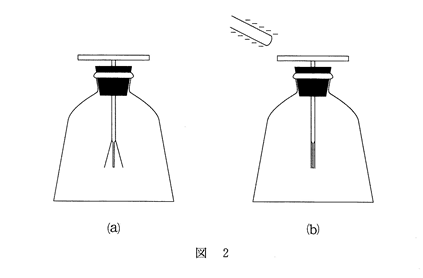
問2 箔検電器に電荷$Q$を与えて、図2(a)で示したように箔を開いた状態にしておいた。次に箔検電器の金属板に、負に帯電した塩化ビニル棒を遠方から近づけたところ、箔の開きは次第に減少して図2(b)のように閉じた。初めに与えた電荷$Q$と図2(b)の状態の金属板の部分にある電荷$Q'$にあてはまる式の組合せとして正しいものを、下の①~⑥のうちから一つ選べ。
① \( Q>0 \),\( Q'>0 \)
② \( Q>0 \),\( Q' = 0 \)
③ \( Q>0 \),\( Q'<0 \)
④ \( Q<0 \),\( Q'>0 \)
⑤ \( Q<0 \),\( Q' = 0 \)
⑥ \( Q<0 \),\( Q'<0 \)
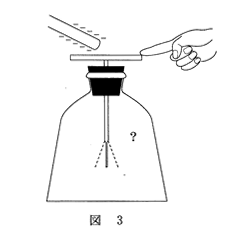
問3 図2(b)の状態からさらに棒を近づけると再び箔は開いた。このとき箔の部分にある電荷は正負いずれか。また、その状態のまま図3のように金属板に指で触れた。指で触れているときの箔の開きは、触れる前と比べてどうなるか。電荷の正負と箔の開き方の組合せとして最も適当なものを、下の①~⑥のうちから一つ選べ。
電荷の正負 |
箔の開き方 |
|
① |
正 |
大きくなる |
② |
正 |
変わらない |
③ |
正 |
小さくなる |
④ |
負 |
大きくなる |
⑤ |
負 |
変わらない |
⑥ |
負 |
小さくなる |
令和2年8月23日
ボーアの水素原子模型
※香川大学の入試問題です。
※入力は次の指示にしたがってください。
- 半角で入力すること。円周率を入力するときは「パイ」をあらわす記号、つまり$π$を使うこと。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。
- 分数の前にマイナスの記号をつけるときは、たとえば5分の2の前にマイナスをつけるならば-2/5のように、分子のところに半角の-を入力すること。
- 累乗は、たとえば「aの2乗」ならa2のように、「○乗」の部分(指数)を直後にそのまま入力すること。
水素原子は、原子核のまわりを、電荷 $-e$〔C〕,質量 $m$〔kg〕の電子1個が、クーロン力 $ke^2/r^2$〔N〕($k$:比例定数)を受けて、速さ$v$〔m/s〕で半径$r$〔m〕の等速円運動をしていると考えられる。この水素原子では、電子の波動性にもとづく物質波(ド・ブロイ波)が、円周上で定常波をつくって安定化していると考えられ、原子のエネルギーはとびとびの値をとる。原子内の電子の状態とエネルギーについて、以下の問いに答えよ。ただし、プランク定数を$h$〔J・s〕とする。
(1) 電子が水素原子核の回りを等速円運動しているときの円運動の方程式を表せ。
(2) この電子の全エネルギー(運動エネルギーと位置エネルギーの和)を表せ。
(3) この水素原子において、電子の波動性にもとづく物質波の波長を表せ。
(4) 電子の物質波が定常波をつくる条件を、量子数$n$を用いて表せ。
(5) 水素原子内の電子が$n$番目の定常状態にあるときの軌道半径$r_n$を、量子数$n$を用いて表せ。
(6) $n$番目の定常状態の原子のエネルギー準位$E_n$を、量子数$n$を用いて表せ。
(7) 水素原子において、基底状態から\( n = 4 \)の励起状態まで電子が励起されたとき、観測しうる線スペクトルの輝線の総数は何本か。
(8) 電子が\( n = 4 \)の励起状態から\( n = 2 \)の状態に遷移したときに放射される電磁波の波長を求めよ。ただし、光の速さを$c$〔m/s〕とする。
