この問題のポイント
同じ直線上で逆向きの2つの力が同じ大きさであるとき、2つの力はつりあう!
3つ以上の力も、x方向・y方向に分解したら逆向きの同じ大きさになる!
問1 物体が別の物体に力を与えている状態をあらわすときは、「どこから(=作用点)」、「どの方向に」「どれぐらいの大きさか」を明らかにしないといけません。これらを簡単に示すために、矢印を使います。つまり、
- 「どこから(=作用点)」…矢印の始点
- 「どの方向に」…矢印の向き
- 「どれぐらいの大きさか」…矢印の長さ
で示すわけですね。この問題では、力の大きさを考えるうえで必要な物体の重さ(この問題では木片やりんご)が与えられていませんから、「どれぐらいの大きさか」以外の点をもとにそれぞれの力について検討していきましょう。
まず、木片にかかる地球からの重力ですが、重力は物体の中心から矢印をひきます。なので、木片の中心から矢印をひきます。そして、重力はふつう鉛直下向きにはたらきますから、矢印は下向きになります。どの選択肢でも、地球からの重力については、すべて同じ矢印となっていますね?
次に、床からの力です。床から木片を押す力(垂直抗力)なのですから、矢印の始点は木片と床との接触面です。そして、床から木片を押すので鉛直上向きに力がかかりますから、矢印は上向きになります。ということは、矢印が下向きになっている①と③は不適です。
最後に、りんごからの力です。矢印の始点は木片とりんごとの接触面です。そして、りんごから木片に力がかかるので鉛直下向きとなるのですから、矢印は下向きになります。よって、矢印がその向きになっている④が正解です。
問2 直感的に「滑車の左側では2個の物体がぶらさがっていて、右側では1個の物体しかないから、ひもの張力は物体1個分と同じ」と解くことができますが、ここでは数式を使って解くとどうなるかを説明していきます。
物体が静止しているということは、はたらいている2つの力がつりあっている状態だということです。つまり、同じ大きさで互いに逆向きの力が同じ直線上ではたらいているということです。
物体A,B,Cにはそれぞれ重力がはたらいています。重力は物体の質量に比例するので、$mg$とあらわすことができます。($m$は質量、$g$は重力加速度)。重力は鉛直下向きにかかる力ですが、同時に下の図のようにひもの張力($S$とおきます)もはたらいています。
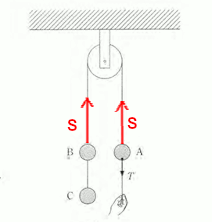
これより、滑車の左側での力のつりあいとして、\( S = mg+mg = 2mg \)
滑車の右側での力のつりあいとして、\( S = mg+T \)が成り立つことになります。
この2つの式より、\( mg+T = 2mg \)
\( ∴T = mg \)
問3 棒の下側には質量$m$の物体があり、これに重力がかかっているわけなので、棒には下向きに$mg$の力がかかっています。そして、棒の上側にはばねがあり、ばねに弾性力(もとの形に戻ろうとする力)がはたらきます。フックの法則より、1本のばねには$kl$(ばね定数×伸びた分の長さ)の弾性力がはたらいています。
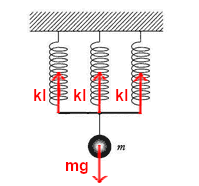
よって、上の図に示された力がはたらいている形でつりあっていることになります。棒にとっては、上向きの力と下向きの力しかはたらいていませんから、3つのばねからの力を1つとみなせば、次の式が成り立ちます。
\( 3kl = mg \)
これを$l$について解くと、\( \displaystyle l = \frac{mg}{3k} \)
問4 この問題では、今までの問題とちがって力が3方向に引っ張られている形でつりあっています。3つ以上の力が成り立っているときは、それぞれの力のベクトルをたすと0ベクトルとなる形になります。これを使って考えることもできますが、ここではもう少し簡単な方法で解いてみましょう。
3つ以上の力が成り立っているとき、それぞれの力を$x$成分だけ,$y$成分だけを足し合わせると0になります。これは言い換えれば、$x$成分だけ,$y$成分に分解したとき、一方向の力を足したものと、逆方向の力を足したものは同じ大きさになるということです。この問題の図を使って具体的に考えましょう。
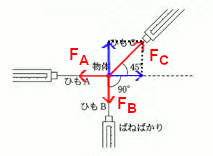
$F_C$だけ斜め向きなので、これを$x$軸方向と$y$軸方向に分解すると、上の図の青い矢印となります。
すると、$x$軸方向の力について\( F_A = F_C\cos45° \)より、\( \displaystyle F_A = \frac{F_C}{\sqrt{2}} \)
$y$軸方向の力について\( F_B = F_C\sin45° \)なので、\( \displaystyle F_B = \frac{F_C}{\sqrt{2}} \)
よって、
$F_A$:$F_B$:$F_C$
= \( \displaystyle \frac{F_C}{\sqrt{2}} \):\( \displaystyle \frac{F_C}{\sqrt{2}} \):$F_C$
= $F_C$:$F_C$:\( \sqrt{2}F_C \)
= \( 1:1:\sqrt{2} \)
答え.
問1 ④ 問2 ④
問3 ① 問4 ②