高校物理の問題演習
円錐面上の等速円運動
※大阪市立大学の入試問題です。
※入力は次の指示にしたがってください。
- 半角で入力すること。根号は「ルート」と入力・変換して出た記号を使うこと。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。
- 累乗は、たとえば「aの2乗」ならa2のように、「○乗」の部分(指数)を直後にそのまま入力すること。
- 根号を使う場合は、たとえば「ルート3」なら√[3]のように、根号の中の部分にあたる部分を[]で囲うこと。
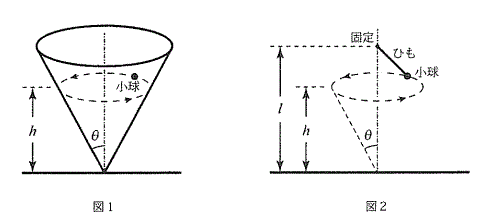
図1のように、鉛直線を中心軸とする半頂角$θ$〔rad〕の円すい面を下向きにし、その頂点を水平な床に固定する。床から高さ$h$〔m〕の位置で、円すいのなめらかな内側の面にそって、水平の向きに速さ$v$〔m/s〕で質量$m$〔kg〕の小球をすべらせると、小球は水平面上を等速円運動した。重力加速度の大きさを$g$〔m/s2〕として、以下の問いに答えよ。
問1 小球の円運動の周期と角速度を、$v$,$h$,$θ$を用いて表せ。
問2 小球の加速度の大きさを、$v$,$h$,$θ$を用いて表せ。また小球が円すい面から受ける垂直抗力の大きさを$N$〔N〕として、円運動の向心力の大きさを、$N$,$θ$を用いて表せ。
問3 垂直抗力の大きさ$N$と速さ$v$を、$m$,$g$,$h$,$θ$のうち必要なものを用いて表せ。
つぎに図2のように円すいを取りはらい、床から高さ$l$〔m〕(\( l>h \))の位置に、軽くて伸びないひもの端を固定し、もう一方の端に質量$m$の小球を付けた。この小球を、高さ$h$の水平面上で速さ$v$の等速円運動をさせたところ、その軌道の半径は、図1の円すい面を円運動する小球と同じであった。
問4 高さ$l$を求めよ。
波の屈折とホイヘンスの原理
※京都大学の入試問題です。
※入力は次の指示にしたがってください。
- すべて半角で入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。
- v2やv3などのような記号はv2やv3のように入力すること。
次の文を読んで、 には適した式を、また、{ }には適切なものの番号を一つ選んで、それぞれの解答欄に記入せよ。
晴れた寒い夜や、上空に強い風が吹いているとき、地上の音源から遠く離れた場所でその音が大きく聞こえることがある。この現象を理解するために、大気の状態を図1のように簡単化して考察してみる。すなわち、水平な2つの境界面(境界面Ⅰおよび境界面Ⅱ)を境にして大気が3つの層から成っており、地表から境界面Ⅰまでの層では音速が$v_1$で無風状態、境界面Ⅰから境界面Ⅱまでの層では音速が$v_2$で無風状態、さらに境界面Ⅱ以上の層では(無風時の)音速が$v_3$であって、風速$w$の風が左から右に向かって水平方向に吹いているとする。この状況において、地上の音源$X$より、鉛直から右へ角度$θ_1$をなす方向に発せられた音波の、各境界面での屈折・反射を考えよう。境界面Ⅰでの音波の屈折角を$θ_2$,境界面Ⅱでの屈折角を$θ_3$,反射角を$θ_4$とする。
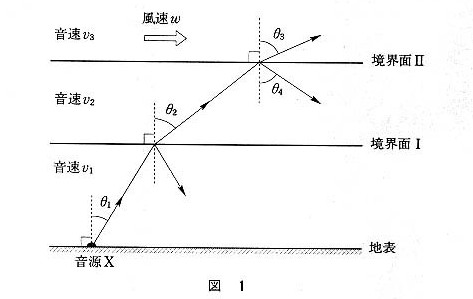
境界面Ⅰは地表から十分離れており、そこに届いた音波は平面波と見なせる。このとき、境界面Ⅰにおける入射角と屈折角の関係を与える式として、\( \displaystyle \frac{v_1}{v_2} \)を$θ_1$,$θ_2$を用いて表す関係式
\( \displaystyle \frac{v_1}{v_2} = \fbox{ア} \)
が成り立つ。
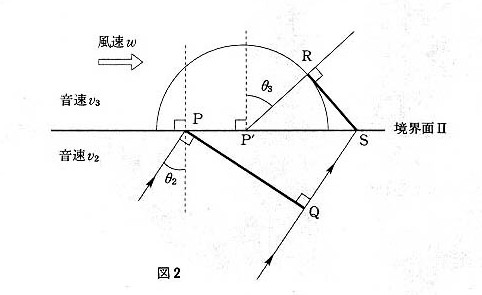
次に、境界面Ⅱにおける入射角と屈折角の間の関係式をホイヘンスの原理にもとづいて考えよう。図2において、速さ$v_2$で進む入射波の波面$PQ$が境界面Ⅱに達すると、$P$から素元波が発せられ球面状に広がっていく。$P$が境界面Ⅱに達してから時間$t$の後、$Q$が境界面上の$S$に達したとする。このとき、$P$から発せられた素元波のなす半円の中心は水平右方向の風のために点$P’$まで移動している。$S$からこの半円に対して引いた接線$RS$が屈折波の波面である。距離\( \overline{PP’} \),\( \overline{P’R} \),\( \overline{QS} \)を$v_2$,$v_3$,$w$,$t$を用いて表すと、
\( \overline{PP’} = \fbox{イ} \)
\( \overline{P’R} = \fbox{ウ} \)
\( \overline{QS} = \fbox{エ} \)
である。したがって、境界面Ⅱでの入射角と屈折角の関係を与える式として、$w$を$θ_2$,$θ_3$,$v_2$,$v_3$を用いて表す関係式
\( w = \fbox{オ} \)
が成り立つ。この境界面Ⅱを透過した屈折波の波面は、鉛直からの角度$θ_3$方向に、$v_3$,$w$,$θ_3$で表される速さ カ で進んでいく。また、境界面Ⅱにおける入射角$θ_2$と反射角$θ_4$の関係を与える式として キ が成り立つ。
さて、音源から遠く離れた地点でその音が大きく聞こえるという現象は、今の場合音源$X$から発せられた音波が境界面で全反射されて地上に返ってくる現象であると考えられる。まず、境界面Ⅰにおける全反射を考えよう。この全反射が起きるような角度$θ_1$が存在するためには、$v_1$,$v_2$に関しての条件
ク <1
が成り立つ必要がある。つまり、境界面ⅠとⅡの間の層の気温が境界面Ⅰ以下の層の気温に比べて{ケ:①高く,②低く}なければならない。この条件が成り立っている場合、\( \sin{θ_A} = \fbox{ク} \)で与えられる角度$θ_A$よりも大きい$θ_1$に対して境界面Ⅰでの全反射が起きる。
原子核と放射線
※( )内の年度のセンター試験の問題です。(答えはすべて半角数字で入力すること)
問1 原子と放射線に関する記述として最も適当なものを、次の①~⑤のうちから一つ選べ。
(2019(平成31))
① 原子の種類(元素)は、原子核内に存在する中性子の数によって決まり、その数を原子番号という。
② 放射線には$α$線,$β$線,$γ$線などがあるが、その透過力や電離作用は放射線の種類によらずほぼ等しい。
③ 私たちは日常生活の中で、食物や空気および大地や宇宙からの自然放射線を浴びている。
④ X線は電場(電界)と磁場(磁界)が進行方向に対して垂直に振動する縦波であり、胸のX線検診では、X線が縦波である性質を利用して、人体組織の疎密を調べている。
⑤ 原子力発電では、核分裂の連鎖反応が継続しないように原子炉を制御しながら、核エネルギーを取り出している。
問2 次の文章中の空欄 ウ ~ オ に入れる語の組合せとして最も適当なものを、下の①~⑧のうちから一つ選べ。
(2016(平成28)・追試)
原子核は正の電荷をもつ ウ と電荷をもたない エ からなる。 ウ や エ は核子と呼ばれ、原子核中の核子の個数を、原子核の オ という。ウランなどの重い原子核が分裂するとき、その前後で核子の総数は変わらないが、質量の総和が減少し、エネルギーが放出される。このエネルギーを電気エネルギーに変換するのが、原子力発電である。
ウ |
エ |
オ |
|
① |
陽子 |
中性子 |
質量数 |
② |
陽子 |
中性子 |
原子番号 |
③ |
陽子 |
ニュートリノ |
質量数 |
④ |
陽子 |
ニュートリノ |
原子番号 |
⑤ |
電子 |
中性子 |
質量数 |
⑥ |
電子 |
中性子 |
原子番号 |
⑦ |
電子 |
ニュートリノ |
質量数 |
⑧ |
電子 |
ニュートリノ |
原子番号 |
磁界と電磁誘導
※( )内の年度のセンター試験の問題です。(答えはすべて半角数字で入力すること)
次の文章(A・B)を読み、下の問い(問1~4)に答えよ。
A 電磁誘導の実験について考えよう。
(2011(平成23))
問1 図4のように銅のリングを糸でつるして静止させ、リングの中心軸に沿って棒磁石を近づける実験を行った。下の文章中の空欄 ア ・ イ に入れる記号,語句の組合せとして最も適当なものを、下の①~④のうちから一つ選べ。
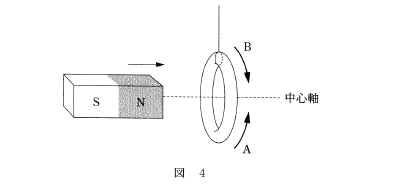
棒磁石のN極をリングに近づけると、リングには図4の ア の矢印の向きに誘導電流が流れる。棒磁石を近づける速さを大きくすると、リングに流れる誘導電流は イ 。
ア |
イ |
|
① |
A |
大きくなる |
② |
A |
小さくなる |
③ |
B |
大きくなる |
④ |
B |
小さくなる |
問2 図5および図6のように、水平な絶縁体の板に置かれた1円玉の真上に、N極を上にして磁石を静止させ、そのあと磁石を鉛直方向にすばやく引き上げた。下の文章中の空欄 ウ ~ オ に入れる記号,語句の組合せとして最も適当なものを、下の①~⑧のうちから一つ選べ。
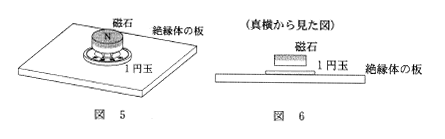
磁石を鉛直上向きに動かすと、1円玉には上から見て図7の ウ の向きの誘導電流が流れる。誘導電流のつくる磁場の向きは1円玉の上面に エ 極をもつ磁石の磁場の向きと同じであるので、1円玉には磁石から オ の力がはたらく。
B 電流が磁場から受ける力と電磁誘導について考える。
(2012(平成24))
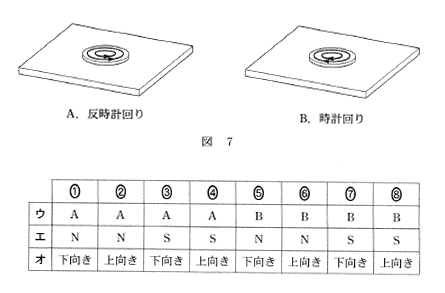
問3 図1のように、水平に置かれた正方形のコイルに、鉛直上向きの一様な磁場がかかっている。コイルには図1に示した向きに電流が流れている。コイルの各辺が磁場から受ける力の向きを表す図として最も適当なものを、下の①~④のうちから一つ選べ。
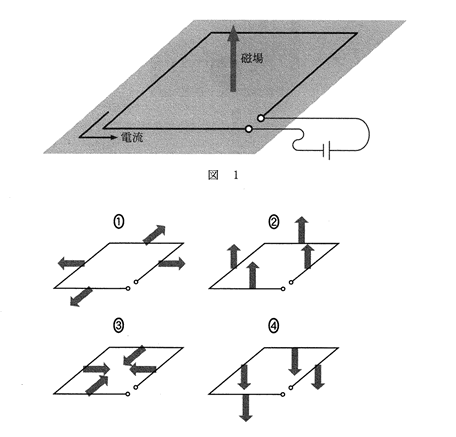
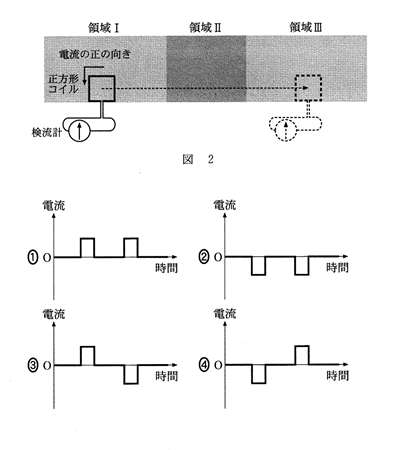
問4 図2のように、検流計をつないだ正方形のコイルを、領域Ⅰから領域Ⅲまで右向きに一定の速さで動かした。領域Ⅰ,Ⅱ,Ⅲには、紙面に垂直に裏から表に向かって磁場がかかっており、それぞれの領域で一様である。領域Ⅰと領域Ⅲの磁場の大きさは同じであり、領域Ⅱの磁場の大きさは領域Ⅰ,Ⅲに比べて大きい。コイルに流れる電流を時間の関数として表したグラフとして最も適当なものを、下の①~④のうちから一つ選べ。ただし、図2の実線の矢印で示される向きを、電流の正の向きとする。
放物運動
※京都工芸繊維大学の入試問題です。
※入力は次の指示にしたがってください。
- 日本語の文字は全角で、その他はすべて半角で入力すること。根号は「ルート」と入力・変換して出た記号を使うこと。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。
- 累乗は、たとえば「aの2乗」ならa2のように、「○乗」の部分(指数)を直後にそのまま入力すること。
- 根号を使う場合は、たとえば「ルート3」なら√[3]のように、根号の中の部分にあたる部分を[]で囲うこと。係数がルートのついた数の場合でも√[5]bのように、囲うこと。
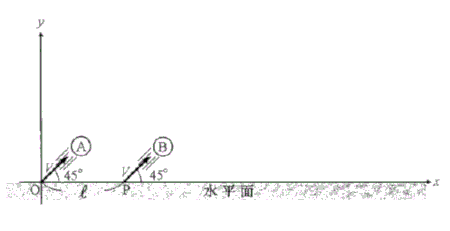
図のような水平で平坦な地面がある。地点$O$を座標原点とし、水平右方向を$x$軸の正方向、鉛直上方を$y$軸の正方向とする。地点$O$から速さ$V$で右側上方45°に向けて質量$m$の球Aを投射した。この時刻を\( t = 0 \)とする。その後、地点$O$から右方向に距離$l$離れた地点$P$から同じ質量$m$の球Bを、球Aと同じ速さ、同じ角度で投射したところ、2つの球A,Bは空中で衝突した。球A,Bは$xy$面内を運動するものとし、球の大きさと空気抵抗は考えない。重力加速度の大きさを$g$として、以下の問いに答えよ。なお、\( \sin45° \)および\( \cos45° \)はともに、小数ではなく\( \displaystyle \frac{1}{\sqrt{2}} \)として解答せよ。
(1) 球Aが衝突前に最高点に到達する時刻(ア)とそのときの高さ(イ)を示せ。
(2) 球Bの投射時刻を示せ。
(3) 衝突する直前の球A,Bの運動エネルギーは、“Aが大きい”、“Bが大きい”、“同じ”のいずれか答えよ。(“”は省いて入力すること)
(4) 衝突時刻を示せ。
(5) 衝突した位置の$x$座標(ア)および$y$座標(イ)を示せ。
