この問題のポイント
屈折・反射・全反射の法則の公式を使えるようになろう!
ホイヘンスの原理を利用して図形で考える問題は、直角三角形を見つけて考えるのがポイント!
ア
境界面Ⅰにて音波は屈折しています。よって、境界面Ⅰに到達する前と後とで、屈折の法則を使うことができます。屈折の法則の公式は次のようなものでしたね。
境界面に到達する前の波の速さを$v_1$、到達した後の波の速さを$v_2$、入射角を$i$、屈折角を$r$とすると、
\( \displaystyle \frac{\sin{i}}{\sin{r}} = \frac{v_1}{v_2} \)
この法則を利用すると、
\( \displaystyle \frac{v_1}{v_2} = \frac{\sin{θ_1}}{\sin{θ_2}} \)
イ
この問題に使われているホイヘンスの原理とはどのようなものかをまず解説しましょう。ホイヘンスの原理とは、波面の各点から、素元波が生じ、その素元波たちに接する面がつぎの瞬間の波面になっていくというものです。ちなみに、波面とは、波たちのなかで同じ高さの点の集合のことです。
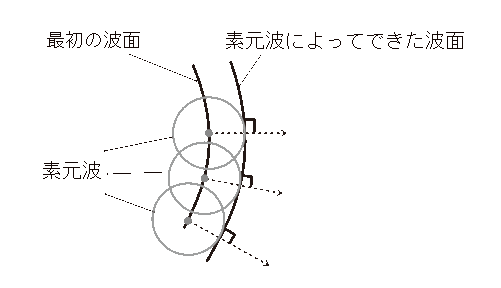
この説明をわかりやすくすると、下の図になります。最初の波面の各点から円形のものが生じていますが、これが素元波です。その素元波の円すべてに接する形の面ができますが、これがつぎの瞬間の波面となるわけです。その波面からも素元波が生じて…という流れで波がどんどん伝わっていくというわけですね。
そして、下の図のとおり、素元波の円の半径と接しているわけですから、波の進行方向と波面は垂直に交わっているということもわかります。
さて、\( \overline{PP’} \)の長さについてですが、これは素元波の中心が風で移動した距離です。時間$t$の間に風速$w$で移動した距離ということになりますから、
\( \overline{PP’} = wt \)
ウ
$P’R$は素元波の半径ですが、問題文の図では素元波の進行方向ともいえます。つまり、素元波がどれだけ進んだかをあらわしているともいえます。境界面Ⅱを超えてからは速さ$v_3$で進み、時間は$t$ですから、
\( \overline{P’R} = v_3t \)
エ
$QS$は波面がどれだけ進んだかをあらわしているともいえますので、それを求めます。境界面Ⅱより下では速さ$v_2$で進んでいて、時間は$t$ですから、
\( \overline{QS} = v_2t \)
オ
現時点でわかっていることは\( \overline{PP’} \),\( \overline{P’R} \),\( \overline{QS} \)という、場所がバラバラの部分の長さだけです。しかし、これだけしか利用できそうなものがありません。
この問題のような、ホイヘンスの原理を利用して図形で考える問題は、直角三角形を見つけて考えるのがポイントです。たとえば、この問題の場合であれば、$△PQS$や$△P’RS$がありますね。この三角形をもとに考えてみましょう。
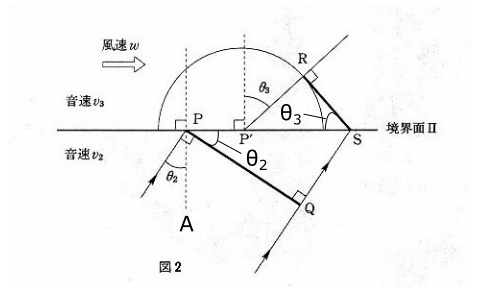
すると、上の図にて、$θ_2$は$90°-∠QPA$ですが、$∠QPS$も$90°-∠QPA$なので、\( ∠QPS = θ_2 \)
同様に、$θ_3$は$90°-∠RP’S$ですが、$∠RSP’$も$90°-∠RP’S$なので、\( ∠RSP’ = θ_3 \)
これより、\( \overline{QS} = \overline{PS}\sin∠QPS \)
\( v_2t = \overline{PS}\sin{θ_2} \)
\( \displaystyle ∴\overline{PS} = \frac{v_2t}{\sin{θ_2}} \)
\( \overline{P’R} = \overline{P’S}\sin∠RSP’ \)
\( v_3t = \overline{P’S}\sin{θ_3} \)
\( \displaystyle ∴\overline{P’S} = \frac{v_3t}{\sin{θ_3}} \)
直角三角形をもとに考えると、この2つの部分の長さがわかりました。
\( \overline{PS} = \overline{PP’}+\overline{P’S} \)ですから、
\( \displaystyle \frac{v_2t}{\sin{θ_2}} = wt+\frac{v_3t}{\sin{θ_3}} \)
\( \displaystyle \frac{v_2}{\sin{θ_2}} = w+\frac{v_3}{\sin{θ_3}} \)
\( \displaystyle ∴w = \frac{v_2}{\sin{θ_2}}-\frac{v_3}{\sin{θ_3}} \)
カ
境界面Ⅱでの屈折なので、屈折の法則を利用した式の形があればいいですね。そこで、オで求めた式を屈折の法則の形に変形してみましょう。すると、
\( \displaystyle \frac{w\sin{θ_3}}{\sin{θ_3}} = \frac{v_2}{\sin{θ_2}}-\frac{v_3}{\sin{θ_3}} \)
\( \displaystyle \frac{w\sin{θ_3}+v_3}{\sin{θ_3}} = \frac{v_2}{\sin{θ_2}} \)
\( \displaystyle \frac{\sin{θ_2}}{\sin{θ_3}} = \frac{v_2}{w\sin{θ_3}+v_3} \)
屈折の法則の形になりましたので、これより、求める速さは\( w\sin{θ_3}+v_3 \)とわかります。
キ
入射角と反射角のことが述べられています。よって、反射の法則を使うことができます。反射の法則の公式は次のようなものです。
入射角を$θ_1$、反射角を$θ_2$とすると、
\( θ_1 = θ_2 \)
(要するに、入射角と反射角は等しい)
この法則を利用すると、\( θ_2 = θ_4 \)です。
ク
屈折せずにすべてが反射して戻ってくることを全反射といいます。その全反射が起こるかどうかのぎりぎりの入射角を臨界角といい、臨界角のときの屈折角はそのまま境界面上を進む形になるので90°となります。
臨界角を$θ_a$として、このときの屈折を、屈折の法則の公式にあてはめていくと、
\( \displaystyle \frac{v_1}{v_2} = \frac{\sin{θ_a}}{\sin90°} \)
これより、\( \displaystyle \sin{θ_a} = \frac{v_1}{v_2} \)
ここで、臨界角は\( 0°<θ_a<90° \)なので、\( \sin{θ_a}<1 \)
\( \displaystyle ∴\frac{v_1}{v_2}<1 \) …㋐
そして、\( θ_a<θ_1<90° \)なので、\( \sin{θ_a}<\sin{θ_1}<1 \)
よって、㋐の式が少なくとも成り立っていないと、全反射が起きるような角度が存在しないことになります。
ケ
音速$V$〔m/s〕と気温$t$〔℃〕の間には、\( V = 331.5+0.6t \)という関係が成り立ちます。つまり、気温が高くなればなるほど、音速は速くなるということです。
\( \displaystyle \frac{v_1}{v_2}<1 \)を変形すると、\( v_1<v_2 \)
ということは、$v_2$のほうが$v_1$より速いわけですから、境界面ⅠとⅡの間の層の気温のほうが高いということになります。よって、正解は①とわかります。
答え.
ア \( \displaystyle \frac{\sin{θ_1}}{\sin{θ_2}} \)
イ $wt$
ウ $v_3t$
エ $v_2t$
オ \( \displaystyle \frac{v_2}{\sin{θ_2}}-\frac{v_3}{\sin{θ_3}} \)
カ \( w\sin{θ_3}+v_3 \)
キ \( θ_2 = θ_4 \)
ク \( \displaystyle \frac{v_1}{v_2} \)
ケ ①