この問題のポイント
円運動の公式を使いこなそう!
等速円運動については、向心力をもとにした運動方程式や、遠心力をもとにした力のつりあいを考える!
問1 円運動についての重要な公式として、以下のものがあります。すべてマスターしておきましょう。
物体が半径$r$[m]の円周上を速さ$v$[m/s]で運動しているとき、
周期\( \displaystyle T[s] = \frac{2πr}{v} \)
角速度\( \displaystyle ω[rad/s] = \frac{θ[rad]}{t[s]} \)
\( v = rω \)
加速度\( a = rω^2 \)
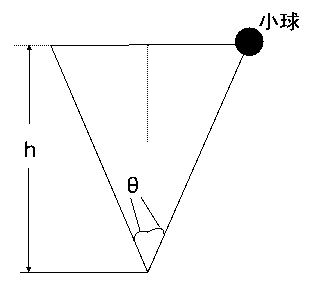
これを利用して、まず周期を考えます。小球が運動している円錐について断面図を描くと右のようになります。ということは、半径は$h\tanθ$とおけるので、公式を利用すると、
周期\( \displaystyle T = \frac{2πh\tanθ}{v} \)
角速度は、上の公式より、回った角度をかかった秒数で割れば求まるとわかります。さっき求めた「周期」というのは、1周するのに何秒の時間がかかるかということです。よって、角速度を$ω$とすると、
\( \displaystyle ω = 2π÷\frac{2πh\tanθ}{v} = \frac{v}{h\tanθ} \)
問2 加速度については、問1の解説にてふれた公式を利用すれば求めることができるでしょう。問1で半径が$h\tanθ$とわかり、角速度も求めたので、加速度を$a$とすると、
\( \displaystyle a = h\tanθ×\left(\frac{v}{h\tanθ}\right)^2 = \frac{v^2}{h\tanθ} \)
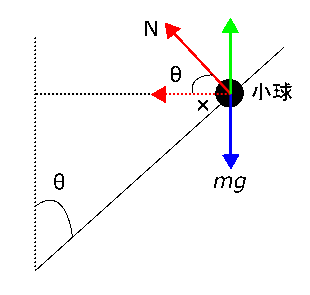
次に、向心力について考えましょう。右の図において、垂直抗力$N$は赤色の実線の矢印、向心力は赤色の点線の矢印ということになります。この向心力は垂直抗力と重力(右の図では青色の矢印)の合力という形になっています。
垂直抗力と向心力の間の角度は右の図より、半頂角の$θ$と同じだと求まります(右の図より、半頂角$θ$は90°-×と求まります。円錐面と垂直抗力$N$がつくる角度も90°なので、垂直抗力と向心力の間の角度も90°-×となり、$θ$と同じになります)。
よって、向心力の大きさは\( N\cosθ \)です。
問3 問2の解説にある図において、重力の方向についての力のつり合いがある(図の青色の矢印と緑色の矢印)ので、
\( mg = N\sinθ \)
\( \displaystyle ∴N = \frac{mg}{\sinθ} \) …①
また、等速円運動については、向心力をもとにした運動方程式か、遠心力をもとにした力のつりあいを考えると、解くことができる問題が多いです。$v$については、運動方程式を使うと求まる手がかりになりそうなので、運動方程式を立ててみましょう。円運動の半径方向の運動方程式は、
\( \displaystyle m\frac{v^2}{r} = F \)
問2にて、向心力は\( N\cosθ \)と求めたので、\( \displaystyle m\frac{v^2}{h\tanθ} = N\cosθ \)
①より、
\( \displaystyle m\frac{v^2}{h\tanθ} = \frac{mg\cosθ}{\sinθ} \)
\( \displaystyle m\frac{v^2}{h\tanθ} = \frac{mg}{\tanθ} \)
\( \displaystyle \frac{v^2}{h\tanθ} = \frac{g}{\tanθ} \)
\( v^2 = gh \)
\( ∴v = \sqrt{gh} \)
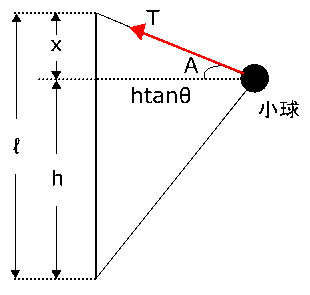
問4 図2での小球の運動を横から見た図が右の図です。この図より、$l$を求めるには、$x$の高さが求まればよいことになります。そこで、問2で考えたところと同じところの角度を$A$とおき、$x$を求める手がかりを考えましょう。
糸の張力を$T$とおきます。まず、問3で考えたのと同じように、重力の方向についての力のつり合いを考えると、
\( mg = T\sin{A} \) …②
そして、問3で考えたのと同じように、円運動の半径方向の運動方程式を考えると、
\( \displaystyle m\frac{v^2}{h\tanθ} = T\cos{A} \) …③
ここで、もし\( \tan{A} \)がわかれば、円運動の半径はわかっているので$x$を求めることができますね?②と③を使って、\( \tan{A} \)を求めてみましょう。
②÷③より、
\( \displaystyle \frac{T\sin{A}}{T\cos{A}} = \frac{mgh\tanθ}{mv^2} \)
\( \displaystyle \tan{A} = \frac{gh\tanθ}{v^2} \)
問3で\( v = \sqrt{gh} \)と求めていたので、
\( \displaystyle \tan{A} = \frac{gh\tanθ}{gh} \)
\( ∴\tan{A} = \tanθ \)(つまり、$A$は$θ$と同じ角度ということです)。
\( \tan{A} \)が求まったので、これを利用すると、
\begin{eqnarray} &&l= h+x\\ &&= h+h\tanθ・\tan{A}\\ &&= h+h\tan^2θ\\ &&= h(1+\tan^2θ)\\ \end{eqnarray}
よって、\( \displaystyle l = \frac{h}{\cos^2θ} \)
答え.
問1
周期…\( \displaystyle \frac{2πh\tanθ}{v} \),
角速度…\( \displaystyle \frac{v}{h\tanθ} \)
問2
加速度…\( \displaystyle \frac{v^2}{h\tanθ} \),
向心力の大きさ…\( N\cosθ \)
問3
\( \displaystyle N = \frac{mg}{\sinθ} \),
\( v = \sqrt{gh} \)
問4
\( \displaystyle l = \frac{h}{\cos^2θ} \)