高校物理の問題演習（４ページ）

高校物理の問題演習

気体の内部エネルギー

※2017（平成29）年のセンター試験の問題です。（答えはすべて半角数字で入力すること）

物質量$n$の単原子分子の理想気体の状態を、図3のように変化させる。過程A→Bは定積変化、過程B→Cは等温変化、過程C→Aは定圧変化である。状態Aの温度を$T_0$、気体定数を$R$とする。

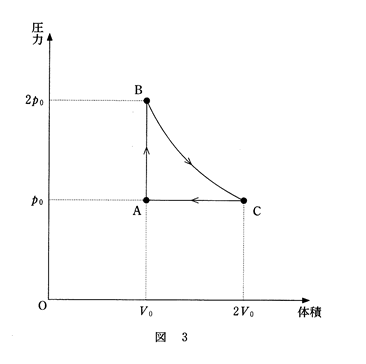
問1　状態Aにおける気体の内部エネルギーは$nRT_0$の何倍か。正しいものを、次の①～⑧のうちから一つ選べ。 1 倍

①　$ \displaystyle \frac{1}{2} $　　　②　1
③　$ \displaystyle \frac{3}{2} $　　　④　2
⑤　$ \displaystyle \frac{5}{2} $　　　⑥　3
⑦　$ \displaystyle \frac{7}{2} $　　　⑧　4

問2　状態Bの温度は$T_0$の何倍か。正しいものを、次の①～⑧のうちから一つ選べ。 2 倍

問3　過程C→Aにおいて気体が放出する熱量は$nRT_0$の何倍か。正しいものを、次の①～⑨のうちから一つ選べ。 3 倍

①　0　　　②　$ \displaystyle \frac{1}{2} $
③　1　　　④　$ \displaystyle \frac{3}{2} $
⑤　2　　　⑥　$ \displaystyle \frac{5}{2} $
⑦　3　　　⑧　$ \displaystyle \frac{7}{2} $
⑨　4

解答・解説はこちら

水圧と浮力

※2007（平成19）年のセンター試験の問題です。（答えはすべて半角数字で入力すること）

図2のように、潜水艇は潜水するときにはバラストタンクに水を導き入れ、浮上するときにはバラストタンクに高圧空気を送り込んで艇外に水を追い出す。バラストタンクを含む潜水艇全体の体積を$V$とし、バラストタンクが空（から）のときの全質量を$M$とする。ただし、水の密度を$ρ$、重力加速度の大きさを$g$とし、空気の質量は無視できるものとする。

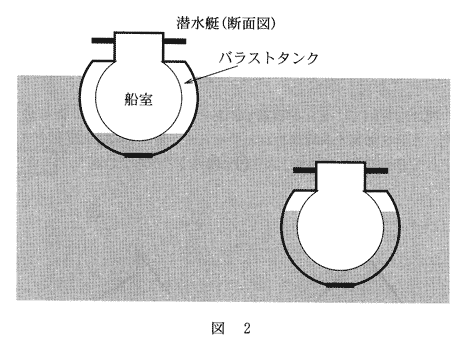
問1　水深100mと200mでの水圧の差は何Pa（＝N/m²）か。最も適当な数値を、次の①～⑥のうちから一つ選べ。ただし、水の密度$ρ$を1.0×10³kg/m³、重力加速度の大きさ$g$を9.8m/s²とする。 1 Pa

①　9.8　　　②　$ 9.8×10^2 $
③　$ 9.8×10^3 $　　　④　$ 9.8×10^4 $
⑤　$ 9.8×10^5 $　　　⑥　$ 9.8×10^6 $

問2　潜水艇が完全に水中にあり、浮力と重力がつりあって静止している。このとき、バラストタンク内の水の体積はいくらか。正しいものを、次の①～⑧のうちから一つ選べ。

①　$ \displaystyle \frac{M}{ρ} $　　　②　$ \displaystyle \frac{M}{ρ}-V $
③　$ \displaystyle V-\frac{M}{ρ} $　　　④　$ \displaystyle \frac{M}{ρ}+V $
⑤　$ \displaystyle \frac{Mg}{ρ} $　　　⑥　$ \displaystyle \frac{Mg}{ρ}-V $
⑦　$ \displaystyle V-\frac{Mg}{ρ} $　　　⑧　$ \displaystyle \frac{Mg}{ρ}+V $

問3　潜水艇がバラストタンクを完全に空（から）にして鉛直に浮上している。このとき、水から受ける抵抗力の大きさは速さ$v$に比例し、比例定数$b$を用いて$bv$と表される。潜水艇の速さが一定になったとき、その速さ$v$はどのように表されるか。正しいものを、次の①～⑥のうちから一つ選べ。
$v$ = 3

①　$ \displaystyle \frac{(ρV+M)g}{b} $　　　②　$ \displaystyle \frac{(ρV-M)g}{b} $
③　$ \displaystyle \frac{ρVg}{b} $　　　④　$ b(ρV+M)g $
⑤　$ b(ρV-M)g $　　　⑥　$ bρVg $

解答・解説はこちら

ドップラー効果

※2017（平成29）年のセンター試験の問題です。（答えはすべて半角数字で入力すること）

音波に関する次の文章を読み、下の問い（問1～3）に答えよ。

音のドップラー効果について考える。音源、観測者、反射板はすべて一直線上に位置しているものとし、空気中の音の速さは$V$とする。また、風は吹いていないものとする。

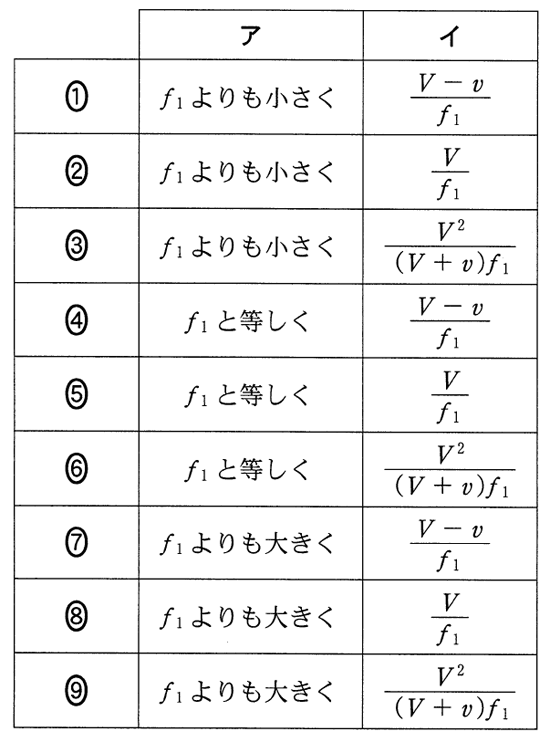
問1　次の文章中の空欄ア・イに入れる語句と式の組合せとして最も適当なものを、下の①～⑨のうちから一つ選べ。

図1のように、静止している振動数$f_1$の音源へ向かって、観測者が速さ$v$で移動している。このとき、観測者に聞こえる音の振動数はア、音源から観測者へ向かう音波の波長はイである。

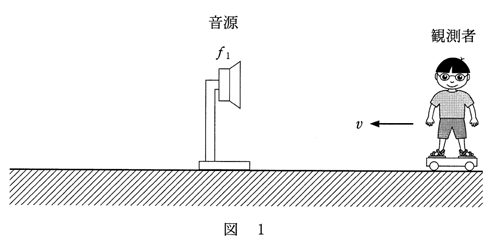
高校　物理　問題演習　ドップラー効果の問題で、静止している音源に向かって観測者が移動している図

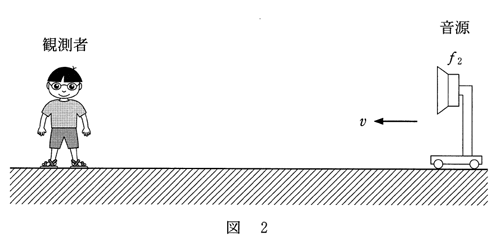
問2　図2のように、静止している観測者へ向かって、振動数$f_2$の音源が速さ$v$で移動している。音源から観測者へ向かう音波の波長$λ$を表す式として正しいものを、下の①～⑤のうちから一つ選べ。$λ$ = 2

高校　物理　問題演習　ドップラー効果の問題で、静止している観測者に向かって音源が移動している図

①　$ \displaystyle \frac{V}{f_2} $
②　$ \displaystyle \frac{V-v}{f_2} $
③　$ \displaystyle \frac{V+v}{f_2} $
④　$ \displaystyle \frac{V^2}{(V-v)f_2} $
⑤　$ \displaystyle \frac{V^2}{(V+v)f_2} $

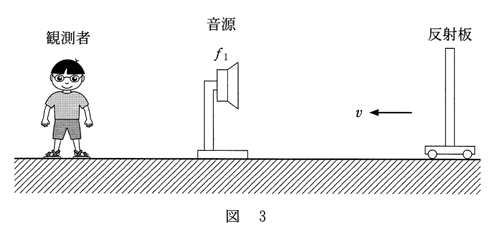
問3　図3のように、静止している振動数$f_1$の音源へ向かって、反射板を速さ$v$で動かした。音源の背後で静止している観測者は、反射板で反射した音を聞いた。その音の振動数は$f_3$であった。反射板の速さ$v$を表す式として正しいものを、下の①～⑧のうちから一つ選べ。$v$ = 3

高校　物理　問題演習　ドップラー効果の問題で、静止している音源に向かって反射板が移動している図

①　$ \displaystyle \frac{f_3-f_1}{f_3+f_1}V $　　　②　$ \displaystyle \frac{f_3+f_1}{f_3-f_1}V $
③　$ \displaystyle \frac{f_3-f_1}{f_1}V $　　　④　$ \displaystyle \frac{f_3-f_1}{f_3}V $
⑤　$ \displaystyle \sqrt{\frac{f_3-f_1}{f_1}}V $　　　⑥　$ \displaystyle \sqrt{\frac{f_3-f_1}{f_3}}V $
⑦　$ \displaystyle \frac{\sqrt{f_3}-\sqrt{f_1}}{\sqrt{f_1}}V $　　　⑧　$ \displaystyle \frac{\sqrt{f_3}-\sqrt{f_1}}{\sqrt{f_3}}V $

解答・解説はこちら

変圧器

※（　　）内の年度のセンター試験の問題を参考に作られています。（答えはすべて半角数字で入力すること）

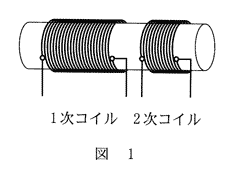
問1　図1のように、鉄心に1次コイルと2次コイルが巻かれている。1次コイルと2次コイルの巻き数の比は2：1である。1次コイルに周波数50Hz、電圧10Vの交流電圧をかけるとき、2次コイルにはどのような交流電圧が生じるか。その周波数と電圧の組合せとして正しいものを、下の①～⑨のうちから一つ選べ。
（2007（平成19））

	周波数〔Hz〕	電圧〔V〕
①	25	5
②	25	10
③	25	20
④	50	5
⑤	50	10
⑥	50	20
⑦	100	5
⑧	100	10
⑨	100	20

問2　変圧器の1次コイルに6600Vの交流電圧を加えたとき、2次コイルには100Vの交流電圧が生じた。1次コイルと2次コイルの巻き数の比はいくらか。最も適当なものを、次の①～⑦のうちから一つ選べ。
1次コイルの巻き数：2次コイルの巻き数 = 1
（2010（平成22））

①　1：4400　　　②　1：66
③　1：8.1　　　④　1：1
⑤　8.1：1　　　⑥　66：1
⑦　4400：1

問3　次の文章中の空欄 2 ・ 3 に入る最も適当な数値を、下の①～⑦のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
（2010（平成22））

発電所で発電された交流の電気は、変圧器により電圧を高くして、送電線を通して送られる。発電所から同じ電力を送るとき、送電線に送り出す電圧（送電電圧）を10倍にすると、送電線を流れる電流は 2 倍になる。この結果、送電線の抵抗によって熱として失われる電力は、 3 倍になる。ただし、送電線の抵抗は変化しないものとする。

①　$ \displaystyle \frac{1}{100} $　　　②　$ \displaystyle \frac{1}{10} $
③　$ \displaystyle \frac{1}{\sqrt{10}} $　　　④　1
⑤　$ \sqrt{10} $　　　⑥　10
⑦　100

解答・解説はこちら

ブラッグ反射

※福岡教育大学の入試問題を参考に作られています。

※入力は次の指示にしたがってください。

記号・ギリシア文字は全角で、その他は半角で入力すること

分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること

負の分数は、たとえばマイナス5分の1なら-1/5のように、-（マイナス）は分子に含めること

分数でない答えは、すべて「2.4×10²」のような有効数字2けたの形で答えること

累乗は、たとえば「aの2乗」ならa2のように、「○乗」の部分（指数）を直後にそのまま入力すること

X線や電子は、波動の性質と粒子の性質を合わせ持つ。ここで波動の性質である波長$λ$と粒子の性質である運動量$p$には、プランク定数を$h$として次の関係式が成り立つ：
$ \displaystyle λ = \frac{h}{p} $

（問1）結晶の構造を求める方法として、X線によるブラッグ反射がある。これと同様の実験が、電子線によっても可能である。この場合、電子線の波長$λ$が、結晶における原子間距離と同程度である必要がある。

銅の結晶における原子間距離は、ほぼ$ 3.6×10^{-10} $mである。電子線の波長を、この原子間距離に一致させるために必要な電子の速さ$v$〔m/s〕の数値を求めよ。なお、$ h = 6.6×10^{-34} $Js，電子の質量を$ m = 9.1×10^{-31} $kgとする。

（問2）電子の速さ$v$を得るため、陽極と陰極の間に電圧をかけて電荷の大きさ$e$を持つ電子を加速する。電子が速さ$v$を得るために必要な電圧$V$を$m$，$v$，$e$を用いて記述せよ。

（問3）（問1）で求めた電子の速さ$v$〔m/s〕を用いて、（問2）の電圧$V$〔V〕の数値を求めよ。ここで電子の電荷を$ e = 1.6×10^{-19} $Cとする。

（問4）波長$λ$の電子線を用いたブラッグ反射は、図3のように反射が起きる格子面どうしの間隔を$d$として、$ 2d\sinθ = nλ $，（$n$ = 1，2，3，…）と表される。$θ$は格子面と入射電子線のなす角度。（格子面と反射電子線のなす角度もこれに等しい。）この入射電子線の運動量の大きさを$d$，$h$，$n$，$θ$を用いて記述せよ。

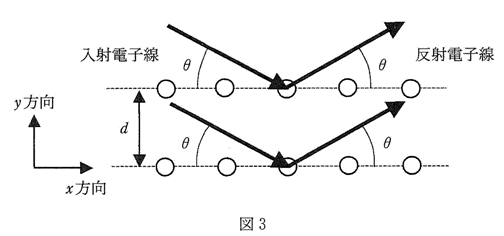
（問5）ここでは、面に垂直で上向きの方向を$y$方向と定義する。入射電子線の運動量の$y$成分、反射電子線の運動量の$y$成分を記述せよ。

解答・解説はこちら

中学・高校の問題演習ができるホームページ