この問題のポイント
X線や電子の波動性をブラッグ反射を通して理解しよう!
格子面どうしの間隔をd、結晶に入り込む角度をθ、波長をλとすると、
2dsinθ = nλ(nは整数)
のとき、お互いに強め合う!
(問1)問題文のリード文に、波長と運動量のことがふれられています。運動量といえば、次のような公式があります。
\( p = mv \)
($p$は運動量〔kg・m/s〕、$m$は質量〔kg〕、$v$は速度〔m/s〕)
よって、リード文にあった、波長$λ$と粒子の性質である運動量$p$の公式は次のように書き換えができることになります。
\( \displaystyle λ = \frac{h}{mv} \)
この問題では、$v$を求めるわけなので、この式を変形すると\( mvλ = h \)なので、
\( \displaystyle v = \frac{h}{mλ} \)
ここでは、波長は原子間距離と等しいという条件になるわけですから、\( λ = 3.6×10^{-10} \)mなので、必要な電子の速さ$v$は、
\( \displaystyle v = \frac{6.6×10^{-34}}{9.1×10^{-31}×3.6×10^{-10}} \)
これを計算していくと、およそ\( v ≒ 2.015×10^6 \)(m/s)となります。この場合は有効数字2けたで答えるのがふつうなので、\( 2.0×10^6 \)(m/s)とすればよいでしょう。
(問2)電子が加速していくということは、その電子は運動エネルギーを持っていると考えることができます。ということは、その運動エネルギーを求めるということで、\( \displaystyle \frac{1}{2}mv^2 \)という公式が利用できるはずです。また、電荷の大きさも与えられているということで、このことを仕事の観点から考えると、電子がやった仕事は$eV$と表すことができます。
この2つは等しい関係にあるわけですから、
\( \displaystyle \frac{1}{2}mv^2 = eV \)
この問題では、$V$について求めていかなければなりませんから、$V$ = …という形に変形していくと、
\( \displaystyle eV = \frac{mv^2}{2} \)
\( \displaystyle V = \frac{mv^2}{2e} \)
(問3)問題文にあるとおり、(問2)で求めた式を利用していくことになります。(問1)で$v$の数値は、\( 2.0×10^6 \)(m/s)と求まりましたが、正確を期して、\( 2.015×10^6 \)を利用することとします。そして、電荷の大きさも、\( e = 1.6×10^{-19} \)Cと与えられています。$m$の数値もわかっているので、これらをすべて代入します。
\( \displaystyle V = \frac{9.1×10^{-31}×(2.015×10^6)^2}{2×1.6×10^{-19}} \)
これを計算すると、$V$ ≒ 1.15×10(V)となります。(問1)で有効数字2けたの形にして答えましたので、ここでもそれに合わせると、1.2×10(V)となります。
(問4)ブラッグ反射というのは、問題文にもあるのですが、電子線やX線が次の条件で結晶に入射したら、電子線やX線はお互いに強め合うということです。
\( 2d\sinθ = nλ \)($n$は整数)
($d$は格子面どうしの間隔、$θ$は結晶に入り込む角度、$λ$は波長)
問題文に書かれていましたが、重要な公式になりますから、覚えておきましょう。
ただ、この問題で求めないといけないのは電子線の運動量です。$h$(プランク定数)を使って表すことが問題文にもありましたが、電子線の運動量については、それを使ったこのような公式がありました。
\( \displaystyle p = \frac{h}{λ} \)
($p$は運動量、$h$はプランク定数、$λ$は波長)
この公式とブラッグ反射の公式を見比べると、どちらも波長$λ$が使われていることがわかります。なので、ここでブラッグ反射の公式を$λ$について解いていくと、
\( nλ = 2d\sinθ \)
\( \displaystyle λ = \frac{2d\sinθ}{n} \)
そして、運動量の公式も$λ$について解くと、
\( pλ = h \)
\( \displaystyle λ = \frac{h}{p} \)
よって、\( \displaystyle \frac{2d\sinθ}{n} = \frac{h}{p} \)
これを$p$について解けばいいわけですから、
\( 2dp\sinθ = nh \)
\( \displaystyle p = \frac{nh}{2d\sinθ} \)
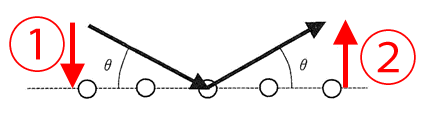
(問5)入射電子線の運動量の$y$成分は右の図でいうと①の矢印、反射電子線の運動量の$y$成分は右の図でいうと②の矢印だということになります。
入射電子線の運動量の大きさを$p$ですから、①の矢印について、ベクトルの大きさとしては\( p\sinθ \)と表せます。さらに、矢印は下向きですから、運動量の大きさは、\( -p\sinθ \)となります。
$p$については、(問4)で$p$ = …と求めた式がありましたから、それを利用しましょう。結局、入射電子線の運動量の$y$成分の大きさは、\( \displaystyle -\frac{nh}{2d\sinθ}×\sinθ = -\frac{nh}{2d} \)です。
反射電子線の運動量の$y$成分も同じ要領で考えればいいでしょう。運動量の大きさは入射電子線と同じですから、$p$ですね。よって、ベクトルの大きさとしては\( p\sinθ \)ですが、②の矢印は上向きですから、運動量の大きさは、さっきとちがって\( p\sinθ \)となります。
そして、(問4)で求めた式を利用して、\( \displaystyle \frac{nh}{2d\sinθ}×\sinθ = \frac{nh}{2d} \)となります。
答え.
(問1)
\( 2.0×10^6 \)(m/s)
(問2)
\( \displaystyle \frac{mv^2}{2e} \)
(問3)
1.2×10(V)
(問4)
\( \displaystyle \frac{nh}{2d\sinθ} \)
(問5)
入射電子線…\( \displaystyle -\frac{nh}{2d} \)
反射電子線…\( \displaystyle \frac{nh}{2d} \)