高校物理の問題演習
鉛直面内の円運動
※上智大学の入試問題です。(数字や記号は半角で入力すること。分数は、分子を入力して/を入力してから分母を入力する形で答え、係数が分数の文字式については、たとえばabの係数が2分の1ならばab/2、abの係数が3分の2ならば2ab/3のように分子の部分に文字を書くこと。根号を使う場合は、√5√abなどと分けずに√[5ab]のような形で入力すること。)
質量$m$の小さなおもりを、長さ$l$の伸び縮みしない軽いひもの一端につけて、他端を点$O$に固定して次の実験を行った。ただし重力加速度を$g$とする。
〔 1 〕~〔 6 〕にあてはまる答えを、記入せよ。ただし、記入は答えのみで、途中の計算式を記入しないこと。
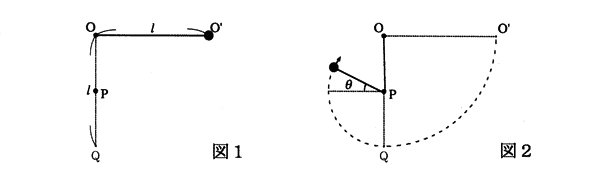
図1のように点$O$の真下にある点$P$にくぎを固定した。点$O$から水平方向に$l$だけ離れた点$O'$で、そっとおもりを放した。
(a) まず\( \displaystyle OP = \frac{l}{2} \)とする。すると、おもりは図2の点線で示すように、最下点$Q$に到達するまでは点$O$を中心とした円軌道を描き、その後は点$P$を中心とした円軌道を描きはじめる。おもりは最下点$Q$に到達したときには、速さ〔 1 〕で運動している。また、ひもの張力は最下点$Q$に到達する直前で〔 2 〕であり、直後には〔 3 〕となる。
その後、図2のように水平から上に角度$θ$だけ回転したときにひもがたるみはじめた。このときの角度$θ$は\( \sinθ \) = 〔 4 〕であたえられ、おもりの速さは〔 5 〕となる。
(b) くぎを打つ点$P$の位置を変化させた。すると、$OP$の距離を〔 6 〕以上にすれば、ひもはたるむことなくおもりは点$P$を中心とした円軌道の一番上まで到達する。
波のグラフ
※日本大学の入試問題を参考に作られています。
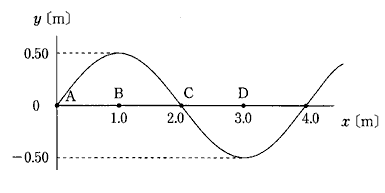
図は$x$軸の正方向に進む横波の正弦波の、ある時刻における波形を表わしている。この波の速さを10〔m/s〕として、次の 1 ~ 7 に答えなさい。ただし、$A$,$B$,$C$,$D$はそれぞれ$x$ = 0.0,1.0,2.0,3.0〔m〕の位置である。(半角数字で入力すること)
(1)この波の振動数は 1 . 2 〔Hz〕である。
(2)図の時刻の直後において、位置$A$,$B$,$C$,$D$の中で媒質が$y$軸の正方向に動くのは 3 である。
(3)図の時刻において、位置$A$,$B$,$C$,$D$の中で媒質の速度が$y$軸の正の向きに最大であるのは 4 である。
(4)図の時刻において、位置$A$,$B$,$C$,$D$の中で媒質の速度が$y$軸の負の向きに最大であるのは 5 である。
(5)図の時刻において、位置$A$,$B$,$C$,$D$の中で媒質の速度が0であるのは 6 である。
〈 3 ~ 6 の解答群〉
① $A$ ② $B$ ③ $C$ ④ $D$ ⑤ $A$と$C$
⑥ $B$と$D$ ⑦ $A$と$B$ ⑧ $C$と$D$
⑨ $A$と$B$と$C$ [0] $A$と$C$と$D$
(6)図の時刻から0.20秒後の位置$B$における変位は 7 〔m〕である。
〈 7 の解答群〉
① 0.50 ② -0.50 ③ 0.00 ④ 0.25
⑤ -0.25 ⑥ 0.71 ⑦ -0.71 ⑧ 0.87
直線電流と磁場
※宮崎大学の入試問題です。
次の文章を読み、設問に対する答えを記せ。
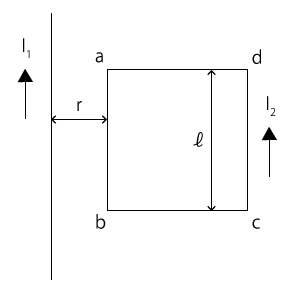
図に示すように、真空中で固定された無限に長く細い直線導線中を、大きさ$I_1$〔A〕をもつ直流電流が矢印の向きに流れている。また、その右側に一辺の長さが$l$〔m〕である正方形の閉じた回路$abcd$が、直線導線と同じ平面上で辺$ab$が直線導線と平行になるように置かれている。このとき、直線導線と辺$ab$の距離は$r$〔m〕であり、真空の透磁率は$μ_0$〔N/A2〕とする。
図に示した正方形回路を動かないように固定する。
(1)回路上、$a$および$d$点における磁束密度の大きさ$B$〔T〕を求めよ。
(2)次に、正方形回路に$a$→$b$→$c$→$d$→$a$の向きに微小な直流電流$I_2$〔A〕を流す。このとき、回路の一辺$ab$が受ける力の大きさ$F_{ab}$〔N〕を求めよ。
(3)同様にして、回路の他の辺$cd$が受ける力の大きさ$F_{cd}$〔N〕を求めよ。
(4)この正方形回路全体が回路のある平面上で直線電流がつくる磁場から受ける力の大きさ$F_1$〔N〕を求めよ。またこの力のはたらく向きを、$b$→$a$,$a$→$b$,$c$→$b$,$b$→$c$のいずれかで答えよ。
ボイル・シャルルの法則
※2004(平成16)年のセンター試験の問題です。
(答えはすべて半角数字で入力すること)
次の文章を読み、下の問い(問1~3)に答えよ。
図1のように、ゴム管でつないだ二つのガラス管$A$と$B$に密度$ρ$の液体が入れてある。ガラス管$A$の上部には栓がついており、はじめ栓は開いている。ガラス管$A$と$B$の断面積を$S$,大気圧を$p_0$,重力加速度の大きさを$g$とする。また、この液体は凝固も蒸発もしないものとする。
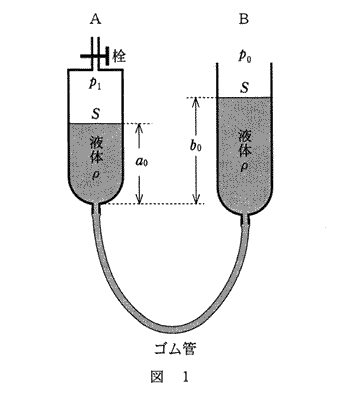
問1 ポンプを用いてガラス管$A$に空気を送り込んだのち、栓を閉じた。そのとき、図1のように、ガラス管$A$と$B$の液面の高さは、ガラス管$A$の底から測ってそれぞれ$a_0$,$b_0$となった。ガラス管$A$に閉じ込められた空気の圧力$p_1$はいくらか。正しいものを、次の①~⑥のうちから一つ選べ。
① \( p_0-(b_0-a_0)ρSg \)
② \( p_0+(b_0-a_0)ρSg \)
③ \( (b_0-a_0)ρSg \)
④ \( p_0-(b_0-a_0)ρg \)
⑤ \( p_0+(b_0-a_0)ρg \)
⑥ \( (b_0-a_0)ρg \)
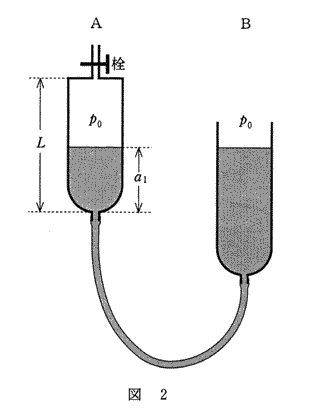
問2 次に、栓を閉じたままガラス管$B$を上下に動かし、ガラス管$A$の液面の高さを変化させることによって、ガラス管$A$に閉じ込められた空気の圧力を変える。図2のように、ガラス管$A$中の空気の圧力を大気圧$p_0$と同じにするための液面の高さを$a_1$とする。$a_1$は、ガラス管$A$の長さ$L$および問1の$a_0$,$p_0$,$p_1$を用いるとどのように表されるか。正しいものを、下の①~④のうちから一つ選べ。ただし、ガラス管に閉じ込められた空気の温度は一定に保たれているものとし、また栓の部分の空気の体積は無視できるものとする。
① \( \displaystyle L-(L-a_0)\frac{p_1}{p_0} \)
② \( \displaystyle L-(L+a_0)\frac{p_1}{p_0} \)
③ \( \displaystyle L-(L-a_0)\frac{p_0}{p_1} \)
④ \( \displaystyle L-(L+a_0)\frac{p_0}{p_1} \)
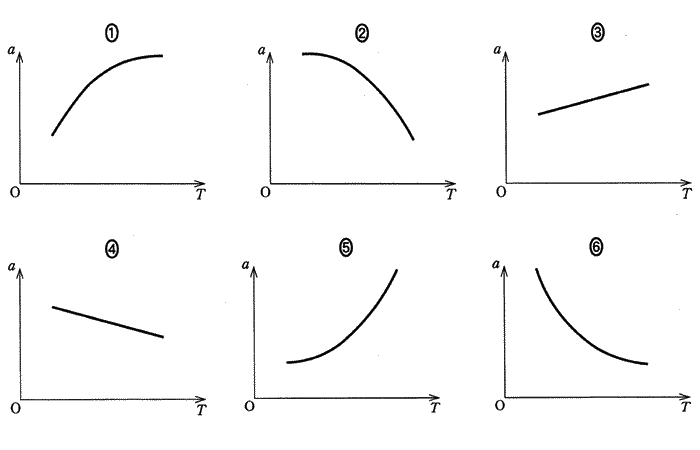
問3 次に、ガラス管$A$に閉じ込められた空気の温度を変化させる。ガラス管$B$を上下させ、ガラス管$B$の液面を$A$の液面と同じ高さに保つようにする。このとき、ガラス管$A$の液面の高さ$a$と閉じ込められた空気の絶対温度$T$の関係はどのようになるか。最も適当なものを、次の①~⑥のうちから一つ選べ。
等加速度運動と相対速度
※学習院大学の入試問題です。
(すべて半角数字で入力すること)
(a)高速道路を自動車$A$が時速108kmで走行している。この速さは秒速何mに相当するか答えよ。
(b)自動車$A$の運転手は危険を感じてブレーキをかけて停止した。ブレーキをかけてから停止するまでの間、自動車$A$は6m/s2で減速したとする。ブレーキをかけてから停止するまでにかかった時間(制動時間)とその間に自動車$A$が走った距離(制動距離)を求めよ。
次に自動車$A$の後ろを自動車$B$が走行している場合を考える。最初、自動車$A$と自動車$B$はともに時速108kmで同じ直線上を走行していたとする。また、このときの車間距離を27mとする。以下の問に答えよ。
(c)自動車$A$の運転手は危険を感じ、ブレーキをかけた。問2と同様に、ブレーキをかけている間は6m/s2で減速する。自動車$B$がブレーキをかけなかった場合、自動車$B$は(自動車$A$がブレーキをかけてから)何秒後に自動車$A$に追突するか。
(d)実際には、自動車$B$は自動車$A$がブレーキをかけてから、1秒後にブレーキをかけた。このときの、自動車$A$との車間距離と、自動車$A$の自動車$B$に対する相対速度を求めよ。
(e)自動車$B$も6m/s2で減速するとする。自動車$B$がブレーキをかけている間、自動車$A$と自動車$B$の車間距離が時間とともにどのように変化するか答えよ。
