問題ページにもどる

この問題のポイント

問1　この問題では、温度や体積などの変化を加えていません。そして、圧力$p_1$のことを問題にしているので、力のつり合いを使いながら考えてみましょう。

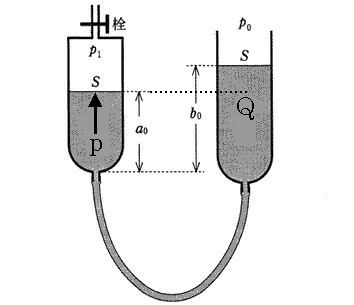
$p_1$はガラス管$A$内の空気の圧力です。これは、上の図の$p$（ガラス管$A$内の液体にある液面での圧力）とつり合っています。ガラス管の断面積は$S$ですから、\( p_1S = pS \)が成り立ちます。
よって、両辺を$S$で割って、\( p_1 = p \)

これはガラス管$B$でも同じことが言えます。上の図のように、ガラス管$A$と同じ高さのところを$Q$とすると、$Q$より下の部分からかかる圧力と、上の部分からかかる圧力は等しいはずです。

$Q$より下の部分の圧力は、ガラス管$A$と同じように考えられますから、$pS$とおけます。
上の部分については、まず、大気圧$p_0$の圧力が断面積$S$のところにかかってますから、$p_0S$の圧力がかかっています。

そして、液体の部分からの圧力もかかっていますが、液体の部分の高さは\( b_0-a_0 \)で、断面積が$S$ですから、液体の部分の体積は\( S(b_0-a_0) \)ですね。密度が$ρ$なんですから、液体の部分の質量は\( (b_0-a_0)ρS \)です。 よって、液体の部分からかかる圧力は\( (b_0-a_0)ρSg \)です。

ということで、$Q$より上の部分からかかる圧力は\( p_0S+(b_0-a_0)ρSg \)なので、
\( pS = p_0S+(b_0-a_0)ρSg \)
両辺を$S$で割って、\( p = p_0+(b_0-a_0)ρg \)

これをさっきの\( p_1 = p \)に代入すると、
\( p_1 = p_0+(b_0-a_0)ρg \)
よって、正解は⑤です。

問2　ガラス管$A$内の空気に着目して考えましょう。この空気は温度はまったく変えられていませんが、圧力を変えているだけなので、これに応じて体積も変わっている形になり、ボイルの法則を使って考えることができます。

つまり、液面が最初の状態（高さ$a_0$）のときと、液面の高さが$a_1$のときでは、ガラス管$A$内の空気について、圧力×体積は同じになります。これを使って方程式をたてましょう。
まず、液面が最初の状態のときの空気の圧力は$p_1$です。そして、液面の高さが$a_1$のときの空気の圧力は$p_0$です。

液面が最初の状態のときの空気の体積ですが、液体の部分の高さが$a_0$なんですから、空気の部分の高さは\( L-a_0 \)で、ガラス管の断面積が$S$ですから、体積は\( S(L-a_0) \)です。
液面の高さが$a_1$のときも同じように考えると、体積は\( S(L-a_1) \)ですね。

これらより、
\( p_1S(L-a_0) = p_0S(L-a_1) \)
\( p_1(L-a_0) = p_0(L-a_1) \)
\( \displaystyle L-a_1 = (L-a_0)\frac{p_1}{p_0} \)
\( \displaystyle -a_1 = -L+(L-a_0)\frac{p_1}{p_0} \)
よって、\( \displaystyle a_1 = L-(L-a_0)\frac{p_1}{p_0} \)

問3　問2とはちがって、この問題では温度が変化しています。なので、シャルルの法則を使って考えていきましょう。まず、温度は$T$とおいておきます。
空気の体積は、問2と同じように考えればいいので、断面積が$S$で高さが$L-a$（$a$は水面の高さ）とおくと、$S(L-a)$と表すことができます。

よって、シャルルの法則を使えば、このように考えることができます。
\( \displaystyle \frac{S(L-a)}{T} = k \)（$k$は定数）

問題のグラフは$T$と$a$を軸にしていますから、上の式を$a$ = …の形に変形していきます。両辺に$T$をかけると、
\( S(L-a) = kT \)となるんですから、
\( \displaystyle L-a = \frac{k}{S}T \)
\( \displaystyle -a = \frac{k}{S}T-L \)
\( \displaystyle a = -\frac{k}{S}T+L \)

これは一次関数の形ですね？ということは、グラフは直線になります。
また、$T$の係数、つまり$T$とかけ算になっている数は－の記号がついているので負の数です。なので、グラフは右下がりの形になります。

右下がりの直線となっているグラフの選択肢は④しかありません。

答え．
問1　⑤　　　問2　①　　　問3　④