この問題のポイント
横軸がxなのかtなのかに注意して、波がどう動くのかをイメージしよう!
振動数と速度の公式は関連づけて覚えよう!
(1)波の振動数$f$の公式と速さ$v$の公式は次のようになります。
周期(1回振動するのに必要な時間)を$T$、波長(波1つの長さ)を$λ$とすると
\( \displaystyle f = \frac{1}{T} \)…①
1回の振動にかかる時間は$T$秒、進む距離は波長の$λ$と同じなので、
\( \displaystyle v = \frac{λ}{T} \)…②
①、②より、
\( v = fλ \)
ちなみに、振動数の単位はHz(ヘルツ)です。
さて、問題文に波の速さは10〔m/s〕と示されていて、さらにグラフから波長は4.0mだとわかりますから、\( v = fλ \)の公式が使えそうですね。
よって、振動数は
\( 10 = f×4.0 \)
\( f = 10÷4 \) = 2.5Hz
(2)波のグラフの問題を解くときは、そのグラフの横軸が$x$なのか$t$なのかをまず確認するようにしましょう。横軸が$x$ならば、ある時刻における波の形、それぞれの地点で媒質がどの位置にあるかを表していて、横軸が$t$ならば、ある地点で媒質が時間とともにどう動いているかを表しています。
この問題では、横軸が$x$なので、波の形、つまりそれぞれの地点でどの位置にあるかが示されています。ですから、時間が前後すれば、そのときの波の形は、このグラフを左右にずらしたのと同じ形になるはずです。(2)については「直後」とありますから、グラフを右に少しずらして考えればよいということになります。
右に少しずらしたとき、それぞれの地点での$y$軸についての目盛りは、
$A$…下がる
$B$…下がる
$C$…上がる
$D$…上がる
$y$軸の正方向に動くということは、$y$軸についての目盛りは上がるわけですから、$C$と$D$において正方向に動くことになります。
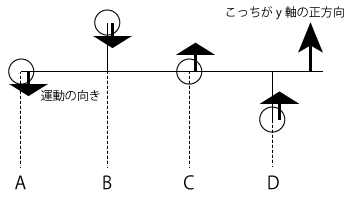
(3)問題文に書いていたとおり、これは横波なんですから、波の進む向きと媒質の動く方向は直角です。そして、(2)でふれたとおり、グラフはそれぞれの地点でどの位置にあるかを示しています。これらのことから、媒質がもし振り子だとすると、それぞれの地点での振り子の動きは、上からみると右図のようになっていると考えられます。
それぞれの地点でどう動いていくのかは(2)で考えたとおりですから、それも書き加えた図になっていますが、速度が$y$軸の正方向のものを選ぶわけですから、$A$と$B$は除外されるということがわかります。
そして、振り子が一番低い位置にきたときが、エネルギーがすべて運動エネルギーに変わるから、速度が最大となります。つまり、振動の真ん中にきているときが、速度が最大となるときなんですから、$C$が条件に一致することになります。
(4)この問題は(3)と同じように考えればいいでしょう。$y$軸の負の向きに動いていくのを選ばないといけないので、$C$と$D$は除外されます。
そして、振動の真ん中にきているのが速度が最大なんですから、$A$が条件に一致しています。
(5)振り子で考えると、速度が0になるのは、一番高い位置のところまでいって逆方向に今からふれようとするときです。つまり、振動の端のところにきているときが、速度が0になっているときです。さっきの図を見ると、一番端にふれているのは$B$と$D$ですから、⑥が正解となります。
(6)この波の速さは10m/sですから、0.20秒後には波は10×0.20 = 2.0m進んでいることになります。よって、波のグラフを2.0m分右にずらして考える必要があります。そうなると、$B$地点にある部分は$D$地点に移り、$A$地点にある部分は$C$地点に移ることになります。
では、$B$地点はもともとどこにあった部分が移ってこられるかと考えると、$A$地点より1.0m前にあった部分が移ってくることになりますね。これは波なんですから、$A$地点より1.0m前の部分では、$D$地点みたいに-0.50mの位置にあることになります。
そして、変位というのは、要するに物体がもともとの位置からどっちの方向にどれだけ動いたかということです。なので、-0.50mの位置にあるということは、変位は-0.50mだということになります。よって、正解は②となります。
答え.
(1) 1 …2 2 …5 (2) ⑧ (3) ③
(4) ① (5) ⑥ (6) ②