この問題のポイント
等速でない円運動は、半径方向の運動方程式と力学的エネルギー保存の法則による方程式を利用して考えよう!
〔 1 〕
点$Q$から見て、高さ$l$のところからの位置エネルギーが、そのまま運動エネルギーに変わったということですから、(点$O'$における位置エネルギー) = (点$Q$における運動エネルギー)という方程式が成り立ちます。よって、
\( \displaystyle mgl = \frac{1}{2}mv^2 \)
\( 2mgl = mv^2 \)
\( v^2 = 2gl \)
\( v>0 \)ですから、\( v = \sqrt{2gl} \) …①
〔 2 〕
おもりは円運動をしています。円運動の問題を解くときに重要な公式があります。
円運動の半径方向の運動方程式
\( \displaystyle F = mrω^2 = m\frac{v^2}{r} \)
($F$は向心力、$m$は質量、$r$は半径、$ω$は角速度(回転する角度)、$v$は速度)
この問題では角速度はわかりませんが、それ以外ならわかりますね?点$Q$に到達する直前では、半径$l$の円運動をしていたわけですから、このときの向心力を$F_A$とすると、こう表せます。
\( \displaystyle F_A = m\frac{v^2}{l} \)
この力を別の観点から考えると、おもりはひもとつながっているんですから、ひもの張力もはたらいていますし、おもり自体にも重力がはたらいています。点$Q$は最下点なんですから、張力はひもが中心へと引っ張ろうとする力となるのに対し、重力は逆に中心から離そうとする力となってはたらきます。
なので、このときのひもの張力を$T_A$とすると、このような式が成り立ちます。
\( \displaystyle m\frac{v^2}{l} = T_A-mg \)
ここで、さっき求めた①を代入すると、
\( \displaystyle m\frac{2gl}{l} = T_A-mg \)
\( 2mg = T_A-mg \)
\( T_A = 3mg \)
〔 3 〕
点$Q$に到達した直後からは、円運動をすることに変わりはないんですが、半径はさっきの半分になります。それが変わっただけで、それ以外については〔 2 〕と同じように考えればよいので、このときの張力を$T_B$とすると、
\( \displaystyle m\frac{v^2}{\frac{l}{2}} = T_B-mg \)
\( \displaystyle m\frac{2v^2}{l} = T_B-mg \)
\( \displaystyle m\frac{2・2gl}{l} = T_B-mg \)
\( 4mg = T_B-mg \)
\( T_B = 5mg \)
〔 4 〕
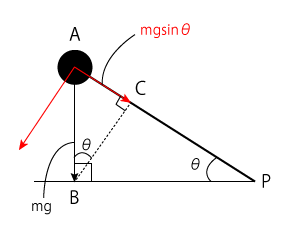
円運動の状態としては、〔 3 〕のときと同じです。このときもひもの張力などがはたらいていますが、そのときの状況を図にしたのが右の図です。
重力$mg$は右の図の赤い矢印で示された2つの分力として分かれます。このとき、ひもの張力と同じ方向にはたらく力の大きさについて考える必要があります。右の図で、$△PAB$と$△BAC$は相似の関係なので、\( ∠ABC = θ \)となり、ひもの張力と同じ方向にはたらく力は\( mg\sinθ \)とあらわせます。
よって、このときのおもりの速さを$v_C$、ひもの張力を$T_C$とすると、半径方向の運動方程式は、
\( \displaystyle m\frac{{v_C}^2}{\frac{l}{2}} = T_C+mg\sinθ \)
ただし、ひもはこのときたるんでいるのですから、張力は0となっています。ですから、この式はこのように変形できます。
\( \displaystyle m\frac{2{v_C}^2}{l} = mg\sinθ \)
\( \displaystyle \frac{2{v_C}^2}{l} = g\sinθ \) …②
ただし、この式だけでは答えを導き出せそうにありません。そこで、このページの一番上に書いたとおり、力学的エネルギー保存の法則を使ってもう1つ方程式を作って考えてみましょう。
最下点$Q$のときの運動エネルギーはそのまま保存されているはずで、そのエネルギーは、ひもがたるんだところでの位置エネルギーと運動エネルギーの和と等しいはずですから、
\( \displaystyle \frac{1}{2}mv^2 = \frac{1}{2}m{v_C}^2+mg\left(\frac{1}{2}l+\frac{1}{2}l\sinθ\right) \)
\( \displaystyle \frac{1}{2}mv^2 = \frac{1}{2}m{v_C}^2+\frac{1}{2}mgl(1+\sinθ) \)
よって、\( v^2 = {v_C}^2+gl(1+\sinθ) \)
①より、\( 2gl = {v_C}^2+gl(1+\sinθ) \)
これより、\( {v_C}^2 = gl-gl\sinθ \) …③
これを②の式に代入すると、
\( \displaystyle \frac{2(gl-gl\sinθ)}{l} = g\sinθ \)
\( \displaystyle \frac{2l(g-g\sinθ)}{l} = g\sinθ \)
\( 2(g-g\sinθ) = g\sinθ \)
\( 2(1-\sinθ) = \sinθ \)
\( 3\sinθ = 2 \)
\( \displaystyle \sinθ = \frac{2}{3} \)
〔 5 〕
$v_C$を求めればいいんですから、〔 4 〕で求めたものを③に代入すれば、
\( \displaystyle {v_C}^2 = gl-gl・\frac{2}{3} = \frac{1}{3}gl \)
\( v_C>0 \)より、\( \displaystyle v_C = \sqrt{\frac{1}{3}gl} \)
〔 6 〕
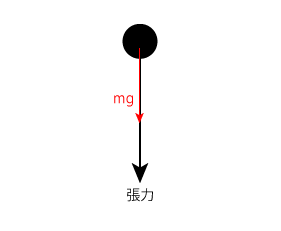
$P$からおもりまでの長さを$L$とすると、おもりは半径$L$の円運動をしたことになります。そして、円軌道の一番上に達した瞬間を図示した右の図を見てわかるとおり、〔 2 〕のときと違って、ひもの張力と重力は同じ方向にはたらいています。
ですから、このときのおもりの速さを$v_D$、張力を$T_D$とすると、半径方向の運動方程式は、
\( \displaystyle m\frac{{v_D}^2}{L} = T_D+mg \)
そして、ひもはたるんではいけないわけですから、$T_D$は0以上でないといけないはずです。つまり、
\( \displaystyle T_D = m\frac{{v_D}^2}{L}-mg≧0 \) …④です。
この問題でも、この運動方程式だけでは解けそうにありませんから、力学的エネルギー保存の法則を使ってもう1つ方程式を作ります。半径が$L$の円運動ですから、円軌道の一番上のところは高さは$2L$となります。よって、〔 4 〕のときのように方程式を作ると、
\( \displaystyle \frac{1}{2}mv^2 = \frac{1}{2}m{v_D}^2+mg・2L \)
\( v^2 = {v_D}^2+4gL \)
①より、\( 2gl = {v_D}^2+4gL \)
\( {v_D}^2 = 2gl-4gL \)
これを④に代入すると、
\( \displaystyle m\frac{2gl-4gL}{L}-mg≧0 \)
\( \displaystyle \frac{m(2gl-4gL)-mgL}{L}≧0 \)
$L$は長さを示しているので、当然\( L>0 \)なので、
\( m(2gl-4gL)-mgL≧0 \)
また、\( m>0 \)なので、\( (2gl-4gL)-gL≧0 \)
\( 5gL≦2gl \)
\( g>0 \)なので、\( \displaystyle L≦\frac{2}{5}l \)
つまり、$P$からおもりまでの長さを、ひも全体の\( \displaystyle \frac{2}{5} \)以下にすればいいということですから、$OP$の長さはひも全体の\( \displaystyle \frac{3}{5} \)以上にすればよいということになります。
答え.
〔 1 〕…\( \sqrt{2gl} \)
〔 2 〕…$3mg$
〔 3 〕…$5mg$
〔 4 〕…\( \displaystyle \frac{2}{3} \)
〔 5 〕…\( \displaystyle \sqrt{\frac{1}{3}gl} \)
〔 6 〕…\( \displaystyle \frac{3}{5}l \)