高校物理の問題演習
コンデンサーと電圧の関係
※東邦大学の入試問題です。
次の文章を読んで、問1と問2に答えよ。
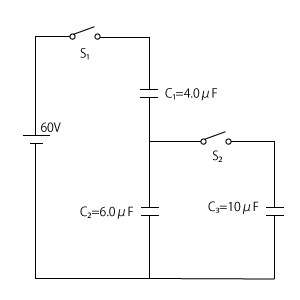
図のような4.0μF,6.0μF,10μFの3つのコンデンサー$C_1$,$C_2$,$C_3$と、60Vの直流電源および$S_1$,$S_2$のスイッチを組み合わせた回路がある。最初、2つのスイッチは開いていて、3つのコンデンサーに電荷は蓄えられてない。
問1 $S_2$を開いたままで、$S_1$を閉じた後、じゅうぶんに時間が経過したときの$C_2$の両端間の電圧はいくらか。(半角アルファベットの小文字で入力すること)
a.12V b.18V c.20V
d.24V e.30V f.36V
問2 その後、$S_1$を開き$S_2$を閉じた後、じゅうぶんに時間が経過したときの$C_3$の両端間の電圧はいくらか。(半角アルファベットの小文字で入力すること)
a.9.0V b.10V c.14V
d.18V e.20V f.24V
原子力発電
※2015(平成27)年のセンター試験の問題です。
次の文章中の空欄( カ )~( ク )に入れる語の組合せとして最も適当なものを、下の①~⑧のうちから一つ選べ(答えは半角数字で入力すること)。
原子力発電ではウランや( カ )などを連鎖的に( キ )させて生じる熱エネルギーを用いる。この核反応では、二酸化炭素は発生しないが、長期にわたって厳重に管理する必要がある( ク )が作り出される。
| カ | キ | ク | |
| ① | ナトリウム | 核融合 | 放射性廃棄物 |
| ② | ナトリウム | 核融合 | 窒素酸化物 |
| ③ | ナトリウム | 核分裂 | 放射性廃棄物 |
| ④ | ナトリウム | 核分裂 | 窒素酸化物 |
| ⑤ | プルトニウム | 核融合 | 放射性廃棄物 |
| ⑥ | プルトニウム | 核融合 | 窒素酸化物 |
| ⑦ | プルトニウム | 核分裂 | 放射性廃棄物 |
| ⑧ | プルトニウム | 核分裂 | 窒素酸化物 |
マイケルソンの干渉計
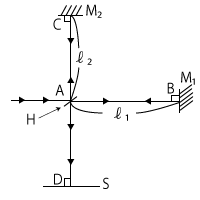
図のように、半透明鏡$H$,2つの鏡$M_1$,$M_2$,スクリーン$S$が真空中に配置されている。$H$の中心$A$と鏡$M_1$の中心$B$との距離は$l_1$,$A$と鏡$M_2$の中心$C$との距離は$l_2$である。図の左側から波長λの平行な光線が$A$に入射し2つに分かれる。一方は、$A$→$B$→$A$→$D$,他方は$A$→$C$→$A$→$D$と進んで両方ともスクリーン上の点$D$に達し、$D$では干渉により明暗が生じた。
(1)点$D$で「明」となる条件を示しなさい。
(2)鏡$M_1$を平行移動し、$B$を$A$のほうに$x$だけ近づけたところ、はじめに「明」であった$D$では明暗を10回くりかえし「明」で止まった。$x$を求めなさい。
(3)$A$と$B$の間に薄透明な窓のついた、内部が真空の容器を挿入し、容器の中に少しずつ空気を入れながら、$D$にできる明暗のくりかえしを数えたところ、1気圧になったときにちょうど$N$回であった。容器の光の通過する部分の厚さを$d$として、1気圧の空気の屈折率$n$を表す式を求めなさい。
比熱と熱量
熱容量が84J/Kの容器の中に120gの水を入れた。これにより全体の温度は20℃で一定になった。その中に、100℃に熱した100gの金属球を入れたところ、全体の温度は30℃になった。このとき、次の問いに答えなさい。ただし、水の比熱は4.2J/(g・K)として計算しなさい。
(1)水の得た熱量は何Jか求めなさい。(半角数字で入力すること)
(2)金属球の比熱を求めなさい。(半角数字で小数第2位まで入力すること)
原子核反応
※宇都宮大学の入試問題を参考に作られています。
陽子$p$を運動エネルギーが\( 1.10×10^6 \)eVになるまで加速し、静止したリチウム原子核$\ce{^{7}_{3}Li}$に当てたところ、核反応
$\ce{p + ^{7}_{3}Li -> ^{4}_{2}He + ^{4}_{2}He}$
により2個の$α$粒子$\ce{^{4}_{2}He}$が発生した。この核反応について以下の問いに答えよ。
(有効数字2けたで答え、累乗の部分はたとえば106ならば「10^6」と入力しなさい)
問1 核反応によって減少した質量[kg]を計算せよ。ただし、陽子、リチウム原子核、$α$粒子の質量をそれぞれ
\( 1.67×10^{-27} \)kg、\( 11.65×10^{-27} \)kg、\( 6.65×10^{-27} \)kg
とする。
問2 減少した質量をエネルギー[J]に換算せよ。真空中の光速を\( 3.00×10^8 \)m/sとする。
問3 核反応後2個の$α$粒子が等しい運動エネルギーを持ったとする。このときの$α$粒子の速さ[m/s]を求めよ。1eV = \( 1.60×10^{-19} \)Jとする。
