中学数学の問題演習
令和4年11月2日
平方根と式の値
※( )内の入試問題で出題された問題です。
※入力は次の指示にしたがってください。
- 半角で入力すること。根号の√は「ルート」で変換して出るものを入力すること。
- 分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること。
- 無理数は、たとえば「ルート3」なら√3のように、√につづけて入力すること。
(1)\( \displaystyle a = \frac{\sqrt{3}+1}{\sqrt{2}} \),\( \displaystyle b = \frac{\sqrt{3}-1}{\sqrt{2}} \)のとき、\( 15a^5b^4÷5a^3b^2 \)の値を求めよ。
(東京・日本大豊山)
(2)\( x = \sqrt{2}+1 \)のとき、\( (x-1)^2(x^2-2x-1) \)の値を求めなさい。
(東京・豊島岡女子学園)
(3)\( x = 4-2\sqrt{3} \),\( y = \sqrt{3}-1 \)のとき、\( x^2+4xy+5y^2+2y+1 \)の値を求めなさい。
(東大寺学園)
(4)\( \displaystyle x = \frac{2\sqrt{3}+\sqrt{7}}{\sqrt{5}} \),\( \displaystyle y = \frac{2\sqrt{3}-\sqrt{7}}{\sqrt{5}} \)のとき、\( x^{12}y^{10}-x^{10}y^{12} \)の値を求めなさい。
(函館ラ・サール)
令和4年8月11日
平行四辺形の性質
※過去の富山県の公立高校入試問題で出題された問題です。(数字やアルファベットは半角で入力すること)
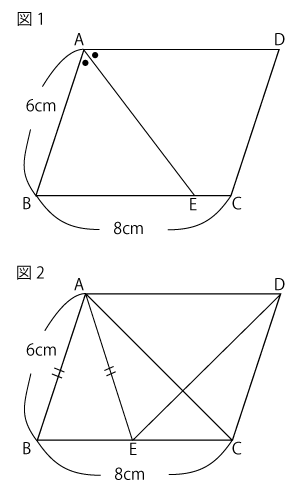
$AB$ = 6cm,$BC$ = 8cmの平行四辺形$ABCD$がある。この平行四辺形の辺$BC$上に点$E$をとり、$A$と$E$を結ぶ。$E$のとり方を(1)~(2)のように変えたとき、次の問いに答えなさい。
(1)図1のように、$AE$が$∠BAD$の二等分線となるように$E$をとるとき、$EC$の長さを求めなさい。
(2)図2のように、$AE = AB$となるように$E$をとり、$A$と$C$,$D$と$E$をそれぞれ結ぶ。
① $△AED$と合同な三角形を2つあげなさい。
② ①であげた2つの三角形のどちらかを選び、$△AED$と合同であることを証明しなさい。
令和4年5月4日
くり返しの規則性
※( )内の高校の入試問題を参考に作られています。(半角数字のみ入力すること)
(1)$2^{2018}$の一の位の数を求めよ。
(茨城・江戸川学園取手)
(2)\( \displaystyle \frac{20}{7} \)を小数で表したとき、小数第200位の数を求めなさい。
(東京・淑徳)
(3)次の問いに答えなさい。
(近畿大和歌山)
① 1から100までのすべての整数を3で割った余りの和を求めなさい。例えば、1から4までのすべての数字を3で割った余りの和は、
1+2+0+1 = 4
である。
② 1から$n$までのすべての整数を5で割った余りの和が96になるような自然数$n$を求めなさい。
令和4年1月20日
二次方程式とその解
※東京都の成城高校の入試問題です。(半角数字のみ入力すること)
$x$についての2次方程式
\( x^2-ax+30 = 0 \)…①
\( x^2-22x+3b = 0 \)…②
がある。$a$,$b$を自然数とするとき、
(1)方程式①が$x = 5$を解にもつような$a$の値は である。
(2)方程式①の解が整数となるような$a$の値は 個ある。
(3)方程式①と②が共通の整数の解をもつような$a$と$b$の値の組は 通りある。
令和3年10月17日
対頂角・同位角・錯角
※( )内の入試問題で出題された問題です。(半角数字のみ入力すること)
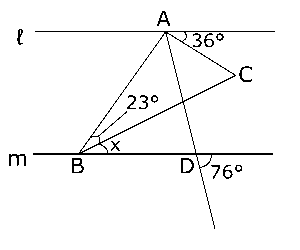
(1)右の図で、2直線ℓ,$m$は平行であり、点$D$は$∠BAC$の二等分線と直線$m$との交点である。このとき、$∠x$の大きさを求めよ。
(京都府公立高校入試)
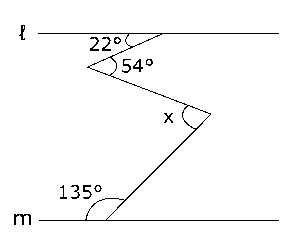
(2)次の図で、ℓ//$m$であるとき、$∠x$の大きさを求めなさい。
(千葉県公立高校入試)
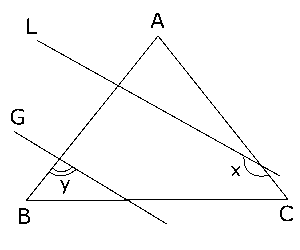
(3)図のように、$△ABC$は$∠A$ = 80°の二等辺三角形で、2直線$L$,$G$は平行である。このとき、\( ∠x+∠y \)を求めなさい。
(東京・明治学院)
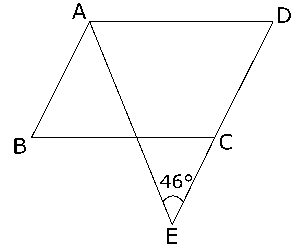
(4)右の図のように、平行四辺形$ABCD$がある。辺$DC$の延長上に点$E$を$∠AED$ = 46°となるようにとったら、\( \displaystyle ∠BAE = \frac{2}{5}∠BAD \)となった。このとき、$∠ADC$の大きさを求めなさい。
(東京・城北)
