この問題のポイント
平行四辺形はそれぞれの対辺が平行→同位角や錯角の性質が使える!
平行四辺形はそれぞれの対辺が等しく、それぞれの対角が等しい!
(1)平行四辺形とは、向かい合った2組の辺が平行な四角形、つまり2組の対辺が平行な四角形のことをいいます。これは小学校の算数でも習ったことですね?
なので、この問題において$AB$//$DC$,$AD$//$BC$が成り立つわけです。平行四辺形が問題で出てきたときは特になのですが、どれとどれが平行になっているかをしっかりつかみましょう。なぜかというと、その平行な2直線による同位角や錯角が問題を解くヒントになることが多いからです。
たとえば、この問題でしたら、$AD$//$BC$なのですから、これにより錯角の関係より
\( ∠DAE = ∠BEA \) …Aとわかります。
そして、$∠DAE$に関係することで、$AE$は$∠BAD$の二等分線でした。よって、
\( ∠DAE = ∠BAE \) …Bです。
A,Bより\( ∠BEA = ∠BAE \)で、この2つの角が等しいので、$△BAE$は$BA = BE$の二等辺三角形とわかります。$BA$の長さは6cmと問題文にありましたから、$BE$も6cmです。よって、$EC$ = $BC-BE$ = 8-6 = 2cmです。
(2)① 合同な三角形の形は同じですから、問題の図を見て$△AED$と似ている形の三角形を考えていくといいでしょう。
もちろん、形が似ている三角形を当てずっぽうで選べばいいというわけではなく、「こことここが等しくて、こことここも等しいから合同になりそうだな」とある程度の根拠をもって考えるようにするべきです。その考え方は②で解説しましょう。
② 合同な三角形について証明するには、どことどこの辺が等しいか、どことどこの角が等しいかを考える必要があります。特に、この問題では平行四辺形の内部にある三角形について考えるわけですが、辺の長さや角の大きさを考えるときに、平行四辺形のこの性質を使うことができます。
1.平行四辺形の2組の対辺がそれぞれ等しい(=向かい合う辺の長さは等しい)
2.平行四辺形の2組の対角がそれぞれ等しい(=向かい合う角の大きさは等しい)
3.対角線はそれぞれの中点で交わる
この問題では2本の対角線がひかれているわけではないので、1.と2.の性質が使えそうですから、これを使ってどんどん等しい辺や角を見つけてみましょう。
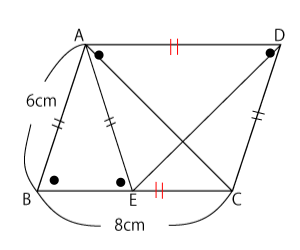
対辺がそれぞれ等しいので、$AD$と$BC$,$AB$と$DC$は等しいですね?さらに、$AE = AB$ということも問題文に書いてあります。
次に、角についてですが、対角がそれぞれ等しいので、$∠ABC$と$∠ADC$,$∠BAD$と$∠BCD$は等しいです。さらに、その$∠ABC$について、$AE = AB$の三角形($△ABE$)の角にもなっているわけですが、そうすると$△ABE$は二等辺三角形になっているわけですから、\( ∠ABC = ∠AEB \)です。さらに、その$∠AEB$においては、(1)で考えたのと同じように、$AD$//$BC$で錯角の関係なので\( ∠AEB = ∠DAE \)です。
ここまでわかった等しい辺や角に印をつけると右の図のようになります。これをもとに考えると、「こことここが等しくて、こことここも等しいから合同になりそうだな」と見当がつきやすいですね。
その図を見て考えると、$△AED$と形が似ている$△BAC$と$△DCA$について、2辺とその間の角がそれぞれ等しいから合同だという証明ができそうですね。
解答のチェックポイント
($△BAC$について証明する場合)
- 平行四辺形の対辺が等しいことを利用して1組の辺が等しいことを証明しているか
- 二等辺三角形の底角や錯角の性質を利用して\( ∠EAD = ∠ABC \)を証明しているか
- 2辺とその間の角がそれぞれ等しいことを根拠に合同であることを証明しているか
($△DCA$について証明する場合)
- 平行四辺形の対辺や二等辺三角形の辺であることを利用して$EA = CD$を証明しているか
- 平行四辺形の対角や二等辺三角形の底角の性質を利用して\( ∠EAD = ∠CDA \)を証明しているか
- 2辺とその間の角がそれぞれ等しいことを根拠に合同であることを証明しているか
答え.
(1)2cm
(2)① $△BAC$,$△DCA$
②(解答例)
($△BAC$について証明するとき)
$△AED$と$△BAC$において、
仮定より、$EA = AB$…①
平行四辺形の対辺は等しいので、$AD = BC$…②
$AD$//$BC$で錯角は等しいので、\( ∠EAD = ∠AEB \)…③
$EA = AB$より$△ABE$は二等辺三角形なので、\( ∠ABC = ∠AEB \)…④
③,④より、\( ∠EAD = ∠ABC \)…⑤
①,②,⑤より、2辺とその間の角がそれぞれ等しいので、
$△AED$≡$△BAC$
($△DCA$について証明するとき)
$△AED$と$△DCA$において、
共通の辺なので、$AD = DA$…①
仮定より、$EA = AB$…②
平行四辺形の対辺は等しいので、$AB = CD$…③
②,③より、$EA = CD$…④
平行四辺形の対角は等しいので、\( ∠CDA = ∠ABC \)…⑤
$EA = AB$より$△ABE$は二等辺三角形なので、\( ∠ABC = ∠AEB \)…⑥
$AD$//$BC$で錯角は等しいので、\( ∠AEB = ∠EAD \)…⑦
⑤,⑥,⑦より、\( ∠EAD = ∠CDA \)…⑧
①,④,⑧より、2辺とその間の角がそれぞれ等しいので、
$△AED$≡$△DCA$