この問題のポイント
対頂角や平行線での同位角・錯角が等しいことを利用して、わかる角度をどんどん書き込む!
角度を書き込んだ角に関係する三角形や四角形を見つけ出すと解きやすくなる!
数学の問題で「ここの角度を求めなさい」という問題があったときは、定理や計算で求まる角度をどんどん書き込んでいくと解くときの大きなヒントになります。今回の問題では、どれも平行な直線が関係していますが、平行な直線に関係する角にはこのような定理があります。
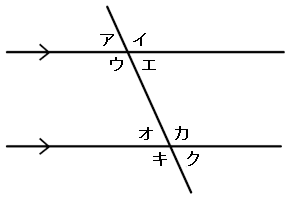
同位角…
2つの直線に別の直線が交わるときに、同じ位置関係でできる角
右の図でのアとオ、イとカ、ウとキ、エとクがそれぞれ同位角である
錯角…
2つの直線に別の直線が交わるときに、交差する位置関係でできる角
右の図でのウとカ、エとオがそれぞれ錯角である
右の図のように、2つの直線が平行なときは同位角は等しい
2つの直線が平行なときは錯角は等しい
逆に、2つの直線の同位角や錯角が等しければ、その2つの直線は平行である
また、平行な直線とは関係しませんが、このような定理もあります。
対頂角…
2本の直線が交わったときにできる、向かい合っている角
どのようなときでも対頂角は等しい
これらの定理を使って実際に問題を解いてみましょう。
(1)まず、対頂角の性質より、$∠ADB$ = 76°です。そして、ℓと$m$は平行で、点$A$のところには$∠ADB$の同位角がありますね?そのうち、36°の角度があるので、$∠DAC$ = 76°-36° = 40°です。さらに、問題文より、$AD$は$∠BAC$の二等分線ですから、$∠BAD$ = $∠DAC$なので、$∠DAC$も40°です。
このように、わかったところすべての角度を問題文の図に書き込んだら、もう一度図を見てみて、角度がもともとわかっている角や自分が角度を求めた角を多く含む三角形や四角形を探してみましょう。たとえば、この問題なら、$△ABD$には$∠ADB$や$∠DAB$の角度が書き込まれていて、3つの角には角度が書かれている状態になっているはずですね?
三角形の内角の和は180°なんですから、
40°+76°+23°+$x$ = 180°
139°+$x$ = 180°
よって、$x$ = 180°-139° = 41°
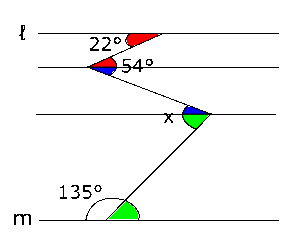
(2)この問題の図では平行線がありますが、間にある線が折れ曲がっているので、同位角や錯角を探し出すことができません。このままだと問題を解くことができませんので、そのようなときは問題を解く手がかりとなる補助線を自分でひく必要があります。そこで、右の図のように、とがっている点を通る平行線を補助線としてひきます。
すると、右の図で同じ色の印がついている角は、それぞれ錯角ということになるので、角度は等しいとわかりますね。よって、まず赤色の印がついている角は22°とわかります。
すると、図を見て明らかなとおり、54°のところは赤色と青色の印があるので、青色の印の角度は54°-22° = 32°です。一方、緑色の印の角については、135°の角と合わせると直線の角度、つまり180°と等しくなるので、角度は180°-135° = 45°です。
$∠x$は青色と緑色の角が合わさった角なので、32°+45° = 77°
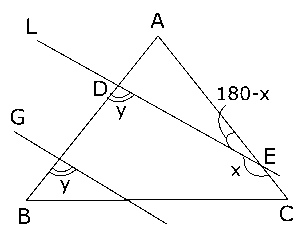
(3)$∠A$ = 80°ということ以外には、$∠x$と$∠y$しか与えられていません。ひとまず、ここからわかる角度を書き込んでいきましょう。
右の図のように直線$L$と$AB$,$AC$それぞれとの交点を$D$,$E$とおきます。$L$と$G$は平行なので、同位角の関係より、$∠BDE = ∠y$です。$∠x$から求まりそうな角については、\( ∠AED = 180°-∠x \)ということだけは求まりそうですね。
ここまで書き込んだところで、角度がもともとわかっている角や自分が角度を求めた角を多く含む図形を探してみると、$△AED$がそれに当てはまりそうですね?$∠BDE$は$△AED$の外角になっていますが、よく見てみると、ちょうど三角形の外角はそれととなり合わない2つの内角の和に等しいという性質が使える状態になっています。
これを利用すると、\( ∠BDE = ∠AED+∠DAE \)なので、
\( ∠y = 180°-∠x+80° \)
\( ∠x+∠y = 180°+80° \)
よって、\( ∠x+∠y = 260° \)
(4)平行四辺形なので、$AD$と$BC$、$AB$と$DC$($DE$)は平行になっています。よって、錯角の関係になっているので、$∠BAE$ = $∠AED$ = 46°と求まります。
\( \displaystyle ∠BAE = \frac{2}{5}∠BAD \)ですから、\( \displaystyle 46° = \frac{2}{5}∠BAD \)なので、
\( \displaystyle ∠BAD = 46°×\frac{5}{2} = 115° \)
これより、$∠EAD$ = 115°-46° = 69°です。
ここまで書き込んだら、角度がもともとわかっている角や自分が角度を求めた角を多く含む図形を探してみます。すると、$△EAD$について、角度が2つわかっているうえに、問題で聞かれている$∠ADC$も$△EAD$の1つの角になっていることがわかりますね?
よって、(1)と同じように、三角形の内角の和は180°ということを利用して、
69°+46°+$∠ADC$ = 180°
115°+$∠ADC$ = 180°
$∠ADC$ = 65°
答え.
(1)41° (2)77°
(3)260° (4)65°