中学数学の問題演習
令和3年7月10日
融合問題(二次関数・確率・立体図形)
※函館ラ・サール高校の入試問題です。
※入力は次の指示にしたがってください。
- 半角で入力すること。円周率$π$は「パイ」で変換して出るものを入力すること。
- 分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること。
- 無理数は、たとえば「ルート3」なら√3のように、√につづけて入力すること。√は「ルート」で変換して出るものを入力すること。
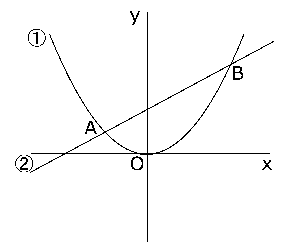
右の図のように、放物線\( y = ax^2 \)…①,直線\( y = bx+3 \)…②が2点$A$,$B$で交わっている。点$A$,$B$の$x$座標はそれぞれ-2,6である。次の問いに答えなさい。
(1)$a$,$b$の値を求めよ。
(2)大,小2つのさいころを同時に投げて、出た目の数をそれぞれ$p$,$q$とする。点\( C(p,q) \)が放物線①と直線②で囲まれた部分(周上の点は除く)にふくまれる確率を求めよ。
(3)$△OAB$を、直線②を軸として1回転させてできる立体の体積を求めよ。ただし、座標の1目もりを1cmとし、円周率は$π$とする。
令和3年4月4日
二次関数と平行四辺形
※東京都の日本大学第二高校の入試問題です。
※入力は次の指示にしたがってください。
- すべて半角のみで入力すること。
- 分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること。文字の係数が分数の場合、xの係数が4分の1ならx/4、yの係数が5分の3なら3y/5のように、分子部分に文字を含めること。
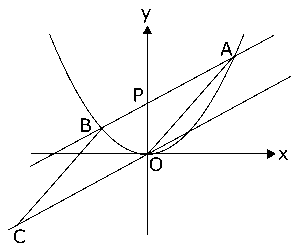
右の図で、直線\( \displaystyle y = \frac{1}{2}x+1 \)は放物線\( \displaystyle y = \frac{1}{2}x^2 \)と2点$A$,$B$で交わり、$y$軸と点$P$で交わっている。いま、直線\( \displaystyle y = \frac{1}{2}x \)上に点$C$をとり、平行四辺形$OABC$をつくるとき、次の問いに答えなさい。
(1)平行四辺形$OABC$の面積を求めなさい。
(2)点$P$を通り平行四辺形$OABC$の面積を2等分する直線の式を求めなさい。
令和2年12月20日
一次関数の式とグラフ
※東京都立産業技術高等専門学校の入試問題です。
※入力は次の指示にしたがってください。
- すべて半角のみで入力すること。
- 不等号は、<は<、>は>、≦は<=、≧は>=と半角で入力すること。
- 分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること。負の分数を入力するときは、たとえば「5分の2」の前にマイナスをつけて-2/5とするように、分子の前に-(マイナス)をつけること。
- 文字の係数が分数の場合、xの係数が4分の1ならx/4、yの係数が5分の3なら3y/5のように、分子部分に文字を含めること。
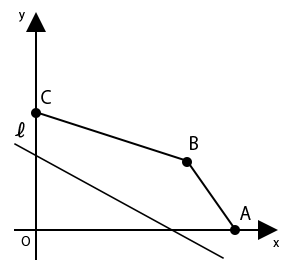
右の図で、点$O$は原点,直線$l$は関数\( \displaystyle y = -\frac{1}{2}x+k \)のグラフを表し、3点$A$,$B$,$C$の座標はそれぞれ(8,0),(6,3),(0,5)である。点$A$と点$B$,点$B$と点$C$をそれぞれ結ぶ。
(1)2点$A$,$B$を通る直線の式を求めなさい。
(2)直線$l$が四角形$OABC$と交わるとき、$k$のとる値の範囲を不等号を使って表しなさい。
令和2年9月6日
比例について
※( )内の入試問題で出題された問題です。
※入力は次の指示にしたがってください。
- すべて半角のみで入力すること。
- 分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること。負の分数を入力するときは、たとえば「5分の2」の前にマイナスをつけて-2/5とするように、分子の前に-(マイナス)をつけること。
$x$ |
□ |
-3 |
0 |
$y$ |
5 |
2 |
0 |
(1)右の表で、$y$が$x$に比例するとき、□にあてはまる数を求めなさい。
(青森県公立高校入試)
(2)プールに
(秋田県公立高校入試)
(3)$y$は$x$に比例し、その比例定数は負の数である。$x$の変域が-6≦$x$≦3のとき、$y$の変域は-7≦$y$≦ になる。 にあてはまる数を求めなさい。
(宮城県公立高校入試)
令和2年5月31日
平行線と線分の比
※東京都の法政大学高校の入試問題です。(半角数字のみで入力すること)
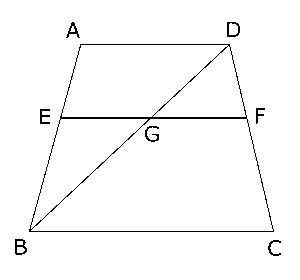
右の図のように、\( AD:BC = 2:3 \)である台形$ABCD$がある。$AB$上の1点$E$から底辺に平行な直線をひき、対角線$BD$および$CD$との交点をそれぞれ$G$,$F$とおく。
(1)\( AE:EB = 1:1 \)となるように点$E$を定めたとき、$EG$:$GF$を最も簡単な整数の比で答えなさい。
(2)\( EG:GF = 2:1 \)となるように点$E$を定めたとき、$AE$:$EB$を最も簡単な整数の比で答えなさい。
