この問題のポイント
放物線や直線の交点ならば、x座標の値を代入して得られるy座標の値は等しい!
軸を1回転させてできる立体では底面である円がどこになるかをみきわめる!
(1)放物線①と直線②の交点について、$x$座標は問題文に書かれています。交点なのですから、放物線①と直線②の方程式の$x$に代入して得られる$y$の値は等しくなるはずですね?
よって、①と②それぞれに\( x = -2 \)を代入したのが等しいので、
\( a×(-2)^2 = b×(-2)+3 \)
\( 4a = -2b+3 \) …ア
①と②それぞれに\( x = 6 \)を代入したのも等しいので、
\( a×6^2 = b×6+3 \)
\( 36a = 6b+3 \) …イ
アとイを連立方程式にして解いていきます。
\(\left\{\begin{array}{l}4a+2b = 3\\36a-6b = 3\end{array}\right.\)
\(\left\{\begin{array}{l}12a+6b = 9\\36a-6b = 3\end{array}\right.\)
\( 12a+6b = 9 \)と\( 36a-6b = 3 \)について、=の左側と右側それぞれで足し算すると、\( 48a = 12 \)となるので、\( \displaystyle a = \frac{1}{4} \)
この$a$の値をアの式に代入すると、
\( \displaystyle 4×\frac{1}{4} = -2b+3 \)
\( 1 = -2b+3 \)
\( 2b = 2 \)
\( b = 1 \)
(2)$a$と$b$の値が(1)で求まりましたので、①の方程式は\( \displaystyle y = \frac{1}{4}x^2 \)、②の方程式は\( y = x+3 \)とわかりました。よって、
$x$が1のとき、①の$y$座標は\( \displaystyle \frac{1}{4}×1^2 = \frac{1}{4} \)、②の$y$座標は1+3 = 4
$x$が2のとき、①の$y$座標は\( \displaystyle \frac{1}{4}×2^2 = 1 \)、②の$y$座標は2+3 = 5
$x$が3のとき、①の$y$座標は\( \displaystyle \frac{1}{4}×3^2 = \frac{9}{4} \)、②の$y$座標は3+3 = 6
$x$が4のとき、①の$y$座標は\( \displaystyle \frac{1}{4}×4^2 = 4 \)、②の$y$座標は4+3 = 7
$x$が5のとき、①の$y$座標は\( \displaystyle \frac{1}{4}×5^2 = \frac{25}{4} \)、②の$y$座標は5+3 = 8
$x$が6のとき、①の$y$座標は\( \displaystyle \frac{1}{4}×6^2 = 9 \)、②の$y$座標も6+3 = 9
さて、大,小2つのさいころについて、それぞれのさいころに1~6までの目があるのですから、\( (p,q) \)は\( (1,1) \)から\( (6,6) \)まで全部で6×6 = 36個が考えられます。
そのなかで、放物線①と直線②で囲まれた部分(周上以外で)にある座標を、さっき「$x$が1のとき…」と考えていったことを参考にひろいあげていくと、
\( (1,1) \),\( (1,2) \),\( (1,3) \)
\( (2,2) \),\( (2,3) \),\( (2,4) \)
\( (3,3) \),\( (3,4) \),\( (3,5) \)
\( (4,5) \),\( (4,6) \)
の11個です。
確率は(条件にあてはまる場合の数)÷(全部の場合の数)で求まりますから、求める確率は\( \displaystyle \frac{11}{36} \)です。
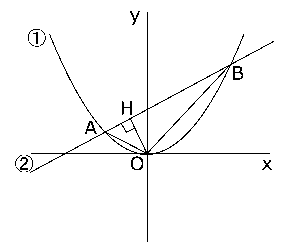
(3)①の方程式は\( \displaystyle y = \frac{1}{4}x^2 \)、②の方程式は\( y = x+3 \)であり、$x$に-2,6を代入すると(①と②どちらに代入してもいいですが)、\( x = -2 \)のとき\( y = 1 \)、\( x = 6 \)のとき\( y = 9 \)なので、$A$の座標は\( (-2,1) \)、$B$の座標は\( (6,9) \)とわかります。
右の図のように、直線②と垂直な直線を$O$からひき、交点を$H$とします。なぜこの$OH$をひいたかというと、$△OAB$を直線②を軸として回転させると、この$OH$を中心にした円ができ、それを底面とした高さ$BH$の円錐と高さ$AH$の円錐がくっついた立体ができるからです。
ということは、この立体の体積を計算するには、底面である円の面積を知るために$OH$の長さを求めることが、まず必要だとわかります。$OH$の長さを求めるために、$H$の座標を考えてみましょう。
直線$OH$と直線②は垂直に交わっていますが、垂直に交わっている直線の傾きの積は-1という性質を利用すれば、直線②の傾きは1ですから、直線$OH$の傾きは-1÷1 = -1
そして、直線$OH$は原点$O$を通るので、中1で習った比例の式\( y = mx \)の形で書けますから、直線$OH$は\( y = -x \)という方程式だとわかります。
よって、\( y = -x \)と直線②の方程式\( y = x+3 \)の連立方程式を解くと、
\( -x = x+3 \)
\( -2x = 3 \)
\( \displaystyle x = -\frac{3}{2} \)
これを\( y = -x \)に代入すると、\( \displaystyle y = -\left(-\frac{3}{2}\right) = \frac{3}{2} \)なので、$H$の座標は\( \displaystyle H\left(-\frac{3}{2},\frac{3}{2}\right) \)
座標がわかる2つの点の距離は√($x$座標の差)2+($y$座標の差)2で求まりますから、
\( \displaystyle OH = \sqrt{\left\{0-\left(-\frac{3}{2}\right)\right\}^2+\left(\frac{3}{2}\right)^2} \)
\( \displaystyle = \sqrt{\left(\frac{3}{2}\right)^2+\left(\frac{3}{2}\right)^2} \)
\( \displaystyle = \sqrt{\frac{9}{4}+\frac{9}{4}} = \sqrt{\frac{18}{4}} = \frac{3\sqrt{2}}{2} \)
なので、$OH$を半径にした円の面積は\( \displaystyle \frac{3\sqrt{2}}{2}×\frac{3\sqrt{2}}{2}×π = \frac{18}{4}π \)とわかるので、立体の体積は、
\( \displaystyle \frac{18}{4}π×BH×\frac{1}{3}+\frac{18}{4}π×AH×\frac{1}{3} \)とおけます。
今度は$BH$と$AH$の長さをそれぞれ求めないといけないと思うかもしれませんが、この式はこのようにすることができます。
\( \displaystyle \frac{18}{4}π×\left(BH×\frac{1}{3}+AH×\frac{1}{3}\right) \)
\( \displaystyle = \frac{18}{4}π×\frac{1}{3}×(BH+AH) \)
$BH$と$AH$をたした長さとは$AB$のことですが、$A$も$B$も座標がわかっていますから、$AB$の長さを求めることができますね?
\( AB = \sqrt{\{6-(-2)\}^2+(9-1)^2} \)
\( = \sqrt{8^2+8^2} = \sqrt{128} = 8\sqrt{2} \)
よって、求める体積は、
\( \displaystyle \frac{18}{4}π×\frac{1}{3}×8\sqrt{2} = 12\sqrt{2}π \)cm3
答え.
(1)\( \displaystyle a = \frac{1}{4} \),\( b = 1 \)
(2)\( \displaystyle \frac{11}{36} \)
(3)\( 12\sqrt{2}π \)cm3