平行線と線分の比－中学・高校の問題演習ができるホームページ

この問題のポイント

どの2直線が平行なのかに注意して、どの線分とどの線分の比が等しいかに着目しよう！

（１）$EG$も$GF$も両方とも直線$EF$上の線分です。平行線がひかれている図形で、1つの直線上にある線分についての比を求める問題では、下の定理を使えることが多いです。

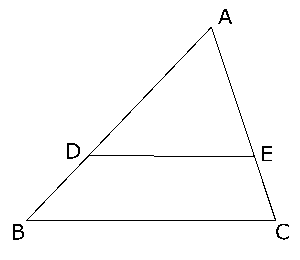
右の図で$DE$//$BC$のとき、
$ AD：AB = AE：AC = DE：BC $
$ AD：DB = AE：EC $

（理由）

$△ABC$と$△ADE$において、$DE$//$BC$より、平行線の同位角は等しいので、
$ ∠ABC = ∠ADE $
$ ∠ACB = ∠AED $
2組の角がそれぞれ等しいので$△ABC$と$△ADE$は相似の関係であり、対応する辺の比が等しいため

この定理を使って$EG$と$GF$の長さを考えてみましょう。

$ AD：BC = 2：3 $なので、$ AD = 2a $，$ BC = 3a $とおきます。$EG$//$AD$ですから、$△BEG$と$△BAD$において、
$ BE：BA = EG：AD $
$ 1：(1+1) = EG：2a $

$ a：b = c：d $ならば$ ad = bc $の関係が成り立つので、
$ 2EG = 2a $
$ EG = a $

また、$△BEG$と$△BAD$において、$ BE：EA = BG：GD = 1：1 $です。

これより、$GF$//$BC$ですから、$△DGF$と$△DBC$において、
$ DG：DB = GF：BC $
$ 1：(1+1) = GF：3a $
$ 2GF = 3a $

よって、$ \displaystyle GF = \frac{3}{2}a $
これより、
$ \displaystyle EG：GF = a：\frac{3}{2}a $
計算していくと、
$ EG：GF = 2a：3a = 2：3 $

（２）$ AE：EB = x：y $とおいて、（１）と同じように考えてみましょう。

$ AD = 2a $，$ BC = 3a $とおき、$△BEG$と$△BAD$について、
$ BE：BA = EG：AD $
$ y：(x+y) = EG：2a $
$ (x+y)EG = 2ay $
$ \displaystyle EG = \frac{2ay}{x+y} $

$△BEG$と$△BAD$において、$ BE：EA = BG：GD = y：x $であり、$△DGF$と$△DBC$において、
$ DG：DB = GF：BC $
$ x：(x+y) = GF：3a $
$ (x+y)GF = 3ax $
$ \displaystyle GF = \frac{3ax}{x+y} $

よって、$ \displaystyle EG：GF = \frac{2ay}{x+y}：\frac{3ax}{x+y} $
これが2：1なのですから、

$ \displaystyle \frac{2ay}{x+y}：\frac{3ax}{x+y} = 2：1 $
$ \displaystyle \frac{2ay}{x+y} = \frac{3ax}{x+y}×2 $
$ 2ay = 3ax×2 $
$ 2y = 6x $
$ y = 3x $

$ AE：EB = x：y $とおいていたのですから、これに代入すると、
$ AE：EB = x：3x = 1：3 $

答え．
（１）$ EG：GF = 2：3 $
（２）$ AE：EB = 1：3 $