この問題のポイント
平行四辺形の対角線の中点を通る直線は、その平行四辺形の面積を2等分する!
(1)平行四辺形の面積は底辺×高さで求まります。ところが、この問題では、底辺も高さもわかりません。よく見ると、平行四辺形$OABC$のかなりの部分が放物線の内側にあります。放物線の内側にある図形は、$y$軸で三角形に分割してその三角形の面積をそれぞれ求めていくと面積が求まることが多いのです。
たとえば、この問題では対角線$OB$をひくと、$△OAB$ができあがりますが、$△OAB$の面積は$△OAP$と$△POB$の面積を求めていけば計算できます。ちょうどこの問題では、$△OAB$は平行四辺形$OABC$のちょうど半分となっています。なので、$△OAB$の面積を求めていくことを考えていきましょう。
放物線\( \displaystyle y = \frac{1}{2}x^2 \)と直線\( \displaystyle y = \frac{1}{2}x+1 \)の交点が$A$,$B$ですから、交点の$x$座標は次の方程式を解けば求まりますね。
\begin{eqnarray} &&\frac{1}{2}x^2 = \frac{1}{2}x+1\\ &&x^2 = x+2\\ &&x^2-x-2 = 0\\ &&(x-2)(x+1) = 0\\ &&x = -1,2 \end{eqnarray}
よって、$A$の$y$座標は\( \displaystyle \frac{1}{2}×2^2 = 2 \)より、$A$の座標は\( (2,2) \),$B$の$y$座標は\( \displaystyle \frac{1}{2}×(-1)^2 = \frac{1}{2} \)より、$B$の座標は\( \displaystyle (-1,\frac{1}{2}) \)とわかりました。
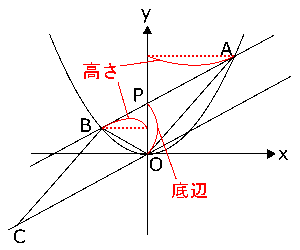
これで、$△OAB$の面積を求める手がかりができました。$△OAP$と$△POB$の面積を考えればいいのですから、$△OAP$と$△POB$の底辺を$OP$とみなせば、$P$の$y$座標は1なので\( OP = 1 \)です。そして、
$△OAP$…右の図より、高さは2となるので、面積は\( \displaystyle 1×2×\frac{1}{2} = 1 \)
$△POB$…右の図より、高さは1となるので、面積は\( \displaystyle 1×1×\frac{1}{2} = \frac{1}{2} \)
よって、$△OAB$の面積は\( \displaystyle 1+\frac{1}{2} = \frac{3}{2} \)
平行四辺形$OABC$の面積はその2倍となるわけなので、\( \displaystyle \frac{3}{2}×2 = 3 \)
(2)直線の式は\( y = ax+b \)であらわすことができますが、$y$軸上にある点$P$を通るわけですから、これが切片となりますね?よって、\( y = ax+1 \)とあらわせます。あとは$a$の値を求めるだけです。
直線は平行四辺形$OABC$の面積を2等分するわけですが、平行四辺形の面積を2等分する直線は必ず対角線の中点を通ります。(1)の問題を考えるときに、対角線$OB$をひきましたから、$OB$の中点を考えてみましょう。
点$O$は原点なので\( (0,0) \)で、点$B$は\( \displaystyle (-1,\frac{1}{2}) \)ですから、2つの点の真ん中の座標は
\( \displaystyle \left(\frac{0-1}{2},\frac{0+\displaystyle\frac{1}{2}}{2}\right) \)、つまり\( \displaystyle \left(-\frac{1}{2},\frac{1}{4}\right) \)
この座標を\( y = ax+1 \)に代入すると、
\( \displaystyle \frac{1}{4} = -\frac{1}{2}a+1 \)
\( 1 = -2a+4 \)
\( 2a = 3 \)
\( \displaystyle a = \frac{3}{2} \)
よって、求める直線の式は\( \displaystyle y = \frac{3}{2}x+1 \)です。
答え.
(1)3
(2)\( \displaystyle y = \frac{3}{2}x+1 \)