この問題のポイント
2組の(x,y)がわかれば、連立方程式を使ってそのグラフの式を求めることができる!
(1)2点$A$,$B$を通るグラフは直線ですから、グラフの式は一次関数\( y = ax+b \)の形であらわすことができます。そして、通っている点の座標がわかっているのですから、それを使って連立方程式をつくれば、そのグラフの式を求めることができます。その求め方を確認しましょう。
$A$の座標が(8,0),$B$の座標が(6,3)ですから、それぞれの$x$座標,$y$座標を\( y = ax+b \)に代入すると、こうなります。
\(\left\{\begin{array}{l}0 = 8a+b\\3 = 6a+b\end{array}\right.\)
このように、$a$,$b$についての連立方程式ができあがります。これを解いていくと、
\(\left\{\begin{array}{l}8a+b = 0 …①\\6a+b = 3 …②\end{array}\right.\)
①-②より、\( 2a = -3 \)
\( \displaystyle a = -\frac{3}{2} \)
これを①に代入すると、\( \displaystyle 8×\left(-\frac{3}{2}\right)+b = 0 \)
\( -12+b = 0 \)より、\( b = 12 \)
$a$,$b$の値が求まったので、求める式は\( \displaystyle y = -\frac{3}{2}x+12 \)です。
(2)$k$とは直線$l$の切片($y$切片)ですから、直線$l$がどう通れば、切片が一番低いところと一番高いところとなるかを考えればいいですね。それを考えるために、2点$B$,$C$を通る直線の式も(1)と同じやり方で求めましょう。
$B$の座標が(6,3),$C$の座標が(0,5)ですから、それぞれの$x$座標,$y$座標を\( y = ax+b \)に代入すると、
\(\left\{\begin{array}{l}3 = 6a+b\\5 = 0a+b\end{array}\right.\)
これを解くと、\( \displaystyle a = -\frac{1}{3} \),\( b = 5 \)
よって、$B$,$C$を通る直線の式は\( \displaystyle y = -\frac{1}{3}x+5 \)
ここで、直線$l$と、$A$,$B$を通る直線、$B$,$C$を通る直線の傾きを比べると、\( \displaystyle -\frac{1}{3}<-\frac{1}{2}<-\frac{3}{2} \)なので、直線$l$の傾きは$B$,$C$を通る直線よりは急ですが、$A$,$B$を通る直線よりはゆるやかということになります。
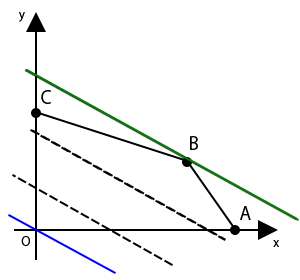
よって、切片が一番低いところとなるのは、直線$l$が原点$O$を通るとき(右の図の青い直線)で、切片が一番高いところとなるのは、直線$l$が点$B$を通るとき(右の図の緑色の直線)とわかります。
原点$O$の座標は(0,0)ですから、それを\( \displaystyle y = -\frac{1}{2}x+k \)に代入すると、
\( \displaystyle 0 = -\frac{1}{2}×0+k \)
\( k = 0 \)
これが$k$の最小値です。
点$B$の座標は(6,3)ですから、それを\( \displaystyle y = -\frac{1}{2}x+k \)に代入すると、
\( \displaystyle 3 = -\frac{1}{2}×6+k \)
\( 3 = -3+k \)
\( k = 6 \)
これが$k$の最大値です。
よって、$k$のとる値の範囲は\( 0≦k≦6 \)です。
答え.
(1)\( \displaystyle y = -\frac{3}{2}x+12 \)
(2)\( 0≦k≦6 \)