中学数学の問題演習
等式の変形
※( )内の入試問題で出題された問題です。
※入力は次の指示にしたがってください。
- 円周率をあらわす記号$π$のみ全角で、それ以外はすべて半角で入力すること。
- 分数は、たとえば分母が4で分子が1なら[1]/[4]、分母が5aで分子が2b+3なら[2b+3]/[5a]のように、それぞれを[]で囲って(分子)/(分母)の形で入力すること。
(1)次の等式を〔 〕の中にある文字について解きなさい。
(ア)\( \displaystyle c = \frac{10a-b}{9}〔b〕 \)
(鹿児島県公立高校入試)
(イ)\( \displaystyle c = b(\frac{1}{a}-2)〔a〕 \)
(明治学院東村山)
(2)等式\( a+3h = 2πh-5b \)を$h$について解きなさい。
(大阪・関西大学第一)
(3)ある中学校の3年A組の人数は36人で、身長の平均は$a$cmである。3年B組の人数はA組より2人多く、身長の平均はA組より2cm低い。3年C組の人数はB組より2人多く、身長の平均はB組より1cm高い。A組とB組とC組をあわせた身長の平均が$b$cmのとき、$a$を$b$の式で表しなさい。
(函館ラ・サール)
式の計算と式の値
※( )内の入試問題で出題された問題です。
※入力は次の指示にしたがってください。
- カタカナのみ全角で、それ以外はすべて半角で入力すること。
- 分数は、たとえば4分の1なら1/4のように、(分子)/(分母)の形で入力すること。
| ㋐ | \( -4a+1 \) | \( 3a+1 \) |
| \( 2a+1 \) | 1 | ㋒ |
| ㋑ | \( 4a+1 \) | \( -a+1 \) |
(1)右の表で、どの縦,横,斜めの3つの式を加えても、和が等しくなるようにしたい。㋐にあてはまる式を求めなさい。
(和歌山県公立高校入試)
(2)2つの式$A$,$B$が\( A = 2x-5y-z \),\( B = -x-7y+2z \)であるとき、3つの式$A$,$B$,$C$について、\( A-3B-C \)を計算したら、\( -2x+5z \)となった。$C$の式を求めなさい。
(東京・筑波大附駒場)
(3)次のア~エのうちから、\( a = -3 \)のときの式の値が、最も小さいものを1つ選び記号で答えなさい。
(千葉県公立高校入試)
ア $-2a$ イ \( a^2+3a-1 \)
ウ \( 2(a+3) \) エ \( \displaystyle \frac{2}{3}a+3 \)
(4)次の式の値を求めなさい。
(東京・早稲田実業)
\( \displaystyle x = \frac{1}{2} \),\( \displaystyle y = -\frac{1}{3} \)のとき、\( \displaystyle \frac{x+y}{2}-\frac{3x-5y}{3}-3y \)
特別な直角三角形の辺の比
※神奈川県の法政大学第二高校の入試問題です。(半角で入力し、無理数は、たとえば「ルート2」なら√2、「ルート3」なら√3と入力すること)
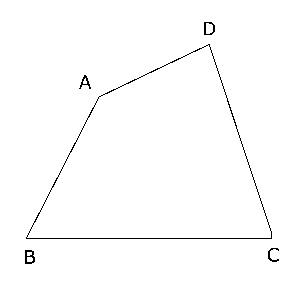
図の四角形$ABCD$において、$∠ABC$ = 60°,$∠BCA$ = 45°,$BC$ = 2である。また、頂点$D$から対角線$AC$に垂線$DH$をひくと、$DH$ = 1である。
(1)頂点$A$から辺$BC$に垂線$AI$をひくとき、線分$AI$の長さを求めなさい。
(2)辺$BC$の延長上に点$P$をとり、四角形$ABCD$の面積と$△ABP$の面積が等しくなるようにするとき、線分$BP$の長さを求めなさい。
~でない確率
※灘高校の入試問題です。(半角のみで入力し、分数は「2分の1」なら1/2のように、(分子)/(分母)の形で入力すること)
3枚のコインを同時に投げるとき、少なくとも1枚のコインが裏となる確率は である。また、3枚のコインを同時に投げることを3回くり返すとき、少なくとも1回はすべてのコインが表となる確率は である。
基本的な作図
※( )内の入試問題で出題された問題です。(解答はこの画面を印刷して作図することをおすすめします)
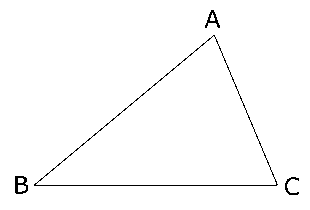
(1)右の図のような$△ABC$がある。頂点$A$を通り、$△ABC$の面積を2等分する直線を右の図に作図しなさい。ただし、作図に用いた線は消さずに残しておくこと。
(愛媛県公立高校入試)
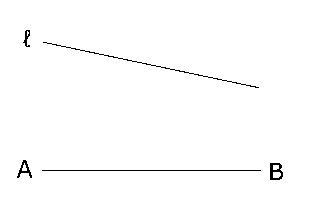
(2)右の図のような線分$AB$と直線ℓがある。線分$AB$の中点を$M$とし、また、直線ℓ上に点$P$をとり、$∠BMP$ = 45°となるようにしたい。点$M$と点$P$を作図によって求めなさい。ただし、作図に用いた線も残しておくこと。
(鹿児島県公立高校入試)
