この問題のポイント
1:1:√2の辺の比、1:2:√3の辺の比を利用して、辺の長さを求めよう!
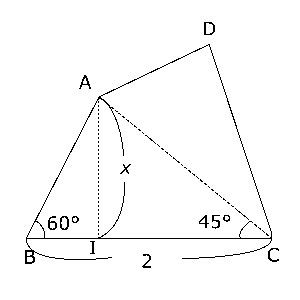
(1)問題文に書かれていることを図にすると右の図のようになります。その図を見ると、$△ABI$や$△AIC$のような直角三角形ができています。直角三角形の辺の長さについては三平方の定理を使って求めることができることがありますが、特に、下の2つの三角形については辺の長さの比が決まっています。
角度が45°、45°、90°の直角三角形は辺の長さの比が$1$:$1$:\( \sqrt{2} \)で、角度が30°、60°、90°の直角三角形は辺の長さの比が$1$:$2$:\( \sqrt{3} \)になっています。図にすると、次のようになります。
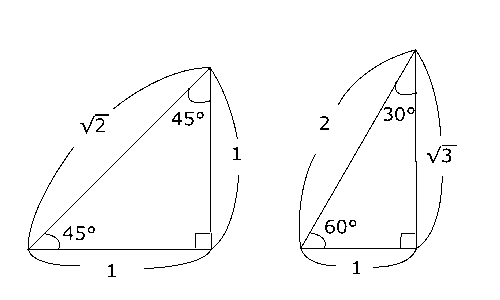
ちょうど、$∠ABC$が60°で、$∠BCA$が45°であり、この辺の比が使えそうですから、その方向で考えてみます。$AI$の長さを$x$とおくと、\( AI:IC = 1:1 \)ですから、\( IC = x \)です。
そして、\( AI:BI = \sqrt{3}:1 \)ですから、
\( \displaystyle BI = \frac{AI}{\sqrt{3}} \)
\( \displaystyle = \frac{x}{\sqrt{3}} \)
\( \displaystyle = \frac{\sqrt{3}x}{3} \)
\( BC = BI+IC \)なので、
\( \displaystyle \frac{\sqrt{3}x}{3}+x = 2 \)
\( \displaystyle \frac{\sqrt{3}x+3x}{3} = 2 \)
\( \displaystyle \frac{(\sqrt{3}+3)x}{3} = 2 \)
\( (\sqrt{3}+3)x = 6 \)となるので、
\( \displaystyle x = \frac{6}{\sqrt{3}+3} \)
\( \displaystyle = \frac{6(\sqrt{3}-3)}{(\sqrt{3}+3)(\sqrt{3}-3)} \)
\( \displaystyle = \frac{6(\sqrt{3}-3)}{3-9} \)
\( \displaystyle = \frac{6(\sqrt{3}-3)}{-6} \)
\( = -(\sqrt{3}-3) \)
\( = 3-\sqrt{3} \)
これが$AI$の長さということになります。
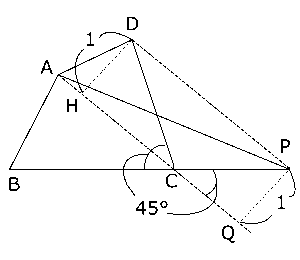
(2)問題文で$AC$の長さについてふれられていますが、$AC$をひくと四角形$ABCD$は2つの三角形に分けることができます。三角形について、平行線の間で底辺を固定して頂点を動かせば、形が変わっても面積が変わらない性質がありました。これを使って四角形$ABCD$と面積が等しい$△ABP$を考えてみましょう。
右の図のように、$AC$と平行な直線$DP$をひいて、$AC$を固定すれば$△ACD$と同じ面積の$△ACP$ができます。これにより、四角形$ABCD$と面積が等しい$△ABP$ができます。あとは$CP$の長さがわかれば、$BP$の長さを求めることができそうですね?
問題文で$DH$の長さについてふれられていましたが、さっきの$AC$と$DP$と同じように、$DH$についても平行な直線をひいてみましょう。$DH$と平行な直線$PQ$をさっきの図のようにひいてみると、$PQ$と$DH$は同じ長さなんですから、\( PQ = 1 \)です。
そして、$△PCQ$にて、対頂角より、$∠PCQ$ = $∠BCA$ = 45°です。ということは、$△PCQ$は(1)にて説明された角度が45°、45°、90°の直角三角形なんですから、\( PQ:CP = 1:\sqrt{2} \)より、\( CP = \sqrt{2} \)です。
よって、
$BP$
\( = BC+CP \)
\( = 2+\sqrt{2} \)
答え.
(1)\( 3-\sqrt{3} \)
(2)\( 2+\sqrt{2} \)