この問題のポイント
垂直を作る垂線、中点を作る垂直二等分線、角を二等分する二等分線の作図のしかたを覚えよう!
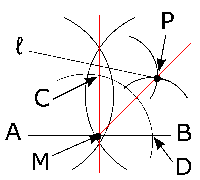
(1)頂点$A$を通るんですから、おそらく作図で求める直線は辺$BC$を通過するはずです。$△ABC$の面積を二等分する直線を考えるわけですが、辺$BC$の真ん中、つまり中点を通ると、$△ABC$の底辺が半分の長さになることになります。底辺が半分になれば、面積も半分になりますよね?
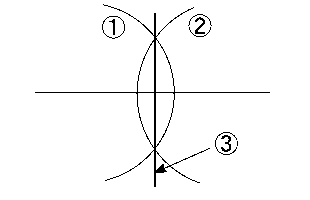
そこで、辺$BC$の中点をまず作図によって求めることになりますが、そこで使えるのが垂直二等分線です。つまり、辺の中点を通って垂直に交わる直線を作図するというわけです。作図のしかたは右の図のようになります。
① 一方の点から弧をコンパスで描く
② もう一方の点から①と同じ半径で弧を描く(つまりコンパスをここではいじらない)
③ 弧が交わっている2点を結ぶ
辺$BC$で作図すると、下の「答え」で示されているように、点$D$を通る垂直二等分線が描けます。この点$D$が辺$BC$の中点なんですから、この点と頂点$A$を結ぶと、求める直線が作図できます。
(2)まず点$M$から作図すべきでしょう。点$M$は線分$AB$の中点ですから、(1)と同じやり方、つまり垂直二等分線の作図をすればいいですね。下の「答え」に示したように、点$A$と点$B$からコンパスで弧を描いて作図します。
次に点$P$です。点$P$は$∠BMP$ = 45°となる点ということがポイントになりそうですね。45°ときたらピンとくるようにしてほしいのですが、これは90°、つまり直角の半分の角度です。ちょうど点$M$を作図するときに垂直二等分線ということで垂線をひきました。この90°を二等分すれば45°をつくることができますね。
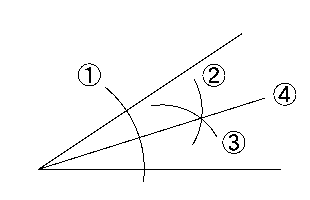
角度を二等分する線、つまり角の二等分線の作図のしかたは右の図のようになります。
① 角の頂点を中心にコンパスで弧を描く
② ①で描いた弧との交点から弧を描く
③ もう一方の交点から②と同じ半径で弧を描く(つまりコンパスをここではいじらない)
④ ②と③で描いた弧の交点と角の頂点を結ぶ
この方法で作図すると、点$M$を中心に弧を描くと、90°の角と弧の交点は、下の「答え」で示されているように、点$C$と点$D$になります。この点$C$と点$D$から弧をまた描いて、というように作図すれば、点$P$が作図できますね。
(重要)
この問題では作図で使うことがありませんでしたが、垂線、つまり線分を二等分する(中点をつくる)必要はないけど垂直な直線をひくときにはどういう作図をすればいいかも確認しましょう。
ふつう、どこかの点から垂線をひくことになるはずですが、その点が垂線をひきたい直線の上にあってもなくても、作図のしかたは同じです。
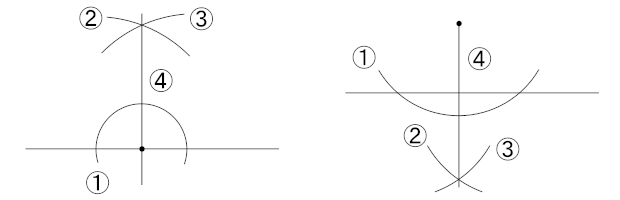
① 垂線をひきたい点を中心にコンパスで弧を描く
② ①で描いた弧との交点から弧を描く
③ もう一方の交点から②と同じ半径で弧を描く(つまりコンパスをここではいじらない)
④ ②と③で描いた弧の交点と垂線をひきたい点を結ぶ
答え.
(1)
下図の赤い直線($D$は書かなくてよい)
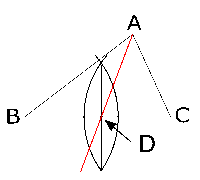
(2)
下図の点$M$と点$P$($C$と$D$は書かなくてよい)