中学数学の問題演習
素因数分解
※過去の大阪教育大学附属高等学校池田校舎の入試問題で出題された問題です。(数字は半角で入力すること)
45を素因数分解すると\( 45 = 3^2×5 \)となる。このとき、素因数3の指数は2であり、素因数5の指数は1である。1から100までのすべての自然数の積を$N$とする。$N$を素因数分解したとき、次の問いに答えなさい。
(1)$N$の素因数の中で次のものを求めなさい。
① 指数が1である最大の素因数
② 指数が2である最大の素因数
③ 指数が5であるすべての素因数(数と数の間は全角の・で区切ること)
(2)素因数3の指数を求めなさい。
連立方程式の係数
※( )内の入試問題で出題された問題です。(半角のみで入力し、分数は「2分の1」なら1/2、「マイナス4分の3」は-3/4などのように記入すること)
(1)2つの$x$,$y$の連立方程式
(i) \(\left\{\begin{array}{l}9bx-2y = -6a\\5x+3y = -1\end{array}\right.\)
(ii) \(\left\{\begin{array}{l}3x+4y = 13\\ax-3by = -6\end{array}\right.\)
がある。
(i)の解$x$,$y$にそれぞれ1を加えたものが(ii)の解である。このとき、定数$a$,$b$の値を求めなさい。
(東京・錦城)
(2)$x$,$y$についての連立方程式
\(\left\{\begin{array}{l}3x+4y = 2\\ax+by = 1\end{array}\right.\)
の解の$x$と$y$を入れかえると、
\(\left\{\begin{array}{l}3x+y = -1\\ax-by = 1\end{array}\right.\)
の解になるという。このとき、定数$a$,$b$の値を求めなさい。
(千葉・東邦大学付属東邦)
(3)$x$,$y$についての連立方程式を解く問題がノートに書いてある。しかし、汚れていて読めない係数があるので、それを$a$とすると、
\(\left\{\begin{array}{l}3x-2y = 17\\ax-4y = 45\end{array}\right.\)
という問題である。係数$a$は整数で、解$x$,$y$はいずれも正の整数であるというが、この問題を解くと、解は$x$ = (1) ,$y$ = (2) であり、読めない係数$a$は (3) だとわかる。
(神奈川・慶應義塾)
2直線の位置関係
※早稲田大学高等学院の入試問題です。
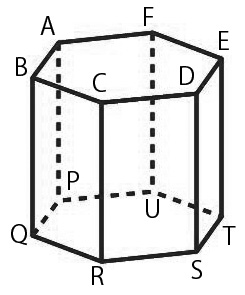
図のような、すべての辺の長さが1である正六角柱$ABCDEF$-$PQRSTU$がある。
(1)直線$AR$と直線$ES$はどのような位置関係にありますか。「交わる」「平行である」「ねじれの位置にある」から選んで答えなさい。(かぎかっこは入力しなくてよい)
(2)この六角柱の底面$ABCDEF$上にある1つの頂点と、底面$PQRSTU$上にある1つの頂点を結んだ直線のうちで、頂点$A$を通る直線と頂点$R$を通る直線を除いたものについて考える。
① このような直線は全部で何本あるか答えなさい。(半角で入力すること)
② このような直線のうちで、直線$AR$と交わる直線は何本あるか答えなさい。また、直線$AR$とねじれの位置にある直線は何本あるか答えなさい。(それぞれ半角で入力すること)
整数部分と小数部分
※( )内の入試問題で出題された問題です。(根号(「ルート」をあらわす記号)は全角で、その他は半角で入力すること)
(1)\(\sqrt{3}\)の小数部分を$a$とするとき、次の式の値を求めなさい。
(青山学院)
\( \displaystyle \frac{a^2-2a}{a-1}÷\frac{a^2-a-2}{a^2-1} \)
(2)\( \displaystyle \frac{\sqrt{5}+2}{\sqrt{3}} \)の整数部分を$a$とするとき、\( (\sqrt{5}+2-a)(\sqrt{5}-2+a) \)の値を求めなさい。
(明治大学付属中野)
二等辺三角形の証明
※京都教育大学附属高校の入試問題です。
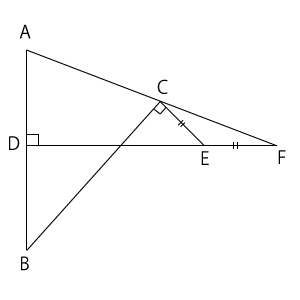
右のような図がある。ただし、点$C$,$D$,$E$はそれぞれ線分$AF$,$AB$,$DF$上にある。また、$∠ADF$ = 90°,$∠BCE$ = 90°,\( EC = EF \)である。このとき、$△ABC$は二等辺三角形であることを証明しなさい。
