中学数学の問題演習
仕事算と一次方程式
※慶應義塾女子高校の入試問題です。
ある仕事をするのに、兄1人ではちょうど18日かかり、弟1人ではちょうど30日かかる。また、2人が力を合わせて働くときは、兄が弟の世話をしながら作業をするため、兄の仕事の速さは10%遅くなるが、弟は50%速くなる。弟が1人で$x$日働いた後、兄が加わって全部でちょうど14日間で仕事を完成させた。$x$の値を求めなさい。(半角で入力すること)
相似の利用
※神奈川県の法政大学第二高校の入試問題です。
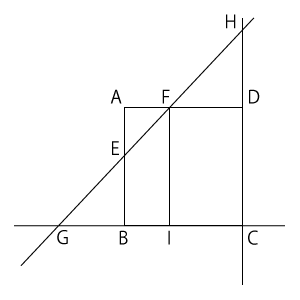
1辺の長さが8の正方形$ABCD$において、辺$AB$,$AD$上にそれぞれ点$E$,$F$をとる。右の図のように、2点$E$,$F$を通る直線と、直線$CB$,$CD$との交点をそれぞれ$G$,$H$とする。また、点$F$から辺$BC$に下ろした垂線の足を$I$とする。\( AF = 3 \),\( AE = a \)(0<$a$<8)であるとき、次の問いに答えなさい。(すべて半角で入力すること)
(1)線分$DH$の長さを$a$を用いて表しなさい。(係数が分数の場合は、たとえばaの係数が4分の3ならば、3a/4のように入力すること。)
(2)$△EGI$の面積を$a$を用いて表しなさい。(答えが分数になる場合は(分子)/(分母)の形で入力し、分母か分子いずれかが多項式になる場合は、展開した形の式にしてその部分を( )でくくること。)
(3)$△EGB$と$△HFD$の相似比が2:1であるとき、$△EBI$の面積は$△HFD$の面積の何倍であるかを求めなさい。((2)と同じルールで入力すること)
合同の証明
※過去の山口県の公立高校入試問題で出題された問題です。
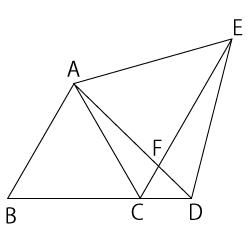
右の図のように、正三角形$ABC$と正三角形$ADE$がある。点$D$は辺$BC$の延長上にあり、辺$AD$と線分$CE$の交点を$F$とする。$△ABD$≡$△ACE$であることを証明しなさい。
正負の数の符号
※( )内の入試問題で出題された問題です。
次の問いに答えなさい。
(1)$a$が正の数で$b$が負の数である。$a$の絶対値より、$b$の絶対値の方が大きいとき、次のア~カの中で、式の値が正になるものをすべて選び記号で答えなさい。(全角カタカナで五十音順に入力すること。記号の間には読点(、)を打つこと)
(奈良育英)
ア $a×b$ イ $a+b$ ウ $a-b$
エ $-a+b$ オ $a^2-b^2$ カ $-a-b$
(2)$a$が正の数,$b$が負の数のとき、つねに正しいものはどれですか。次の㋐~㋓の中から1つ選びなさい。(全角カタカナで入力すること)
(福島県公立高校入試)
㋐ $a+b$の計算の結果は正の数
㋑ $a-b$の計算の結果は正の数
㋒ $a×b$の計算の結果は正の数
㋓ $a÷b$の計算の結果は正の数
二次方程式の簡単な応用
※過去の青森県の公立高校入試問題で出題された問題です。
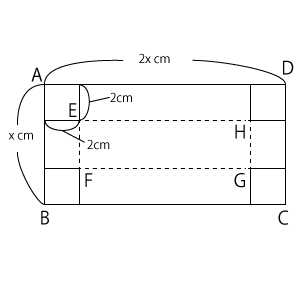
右の図のように、$AB$ = $x$cm、$AD$ = $2x$cmの長方形$ABCD$の厚紙があります。この厚紙の4すみから1辺の長さが2cmの正方形を切り取り、折り曲げて直方体の容器をつくります。ただし$x$>4とします。次の問いに答えなさい。
(1)$EF$の長さを$x$を用いて表しなさい。(半角のみを使用し、文字のある項から入力すること)
(2)この直方体の容器の体積を$x$を用いて表しなさい。(半角のみを使用し、次数の高い項から順にした書き方で入力すること。また、「xの2乗」については「x2」と入力すること)
(3)この直方体の容器の体積が96cm3になるときの$x$の値を求めなさい。(半角のみを使用すること)
