この問題のポイント
簡単にわかる等しい辺や角から、使えそうな合同条件を考えていこう!
重なっている部分がある辺や角は分解して考えよう!
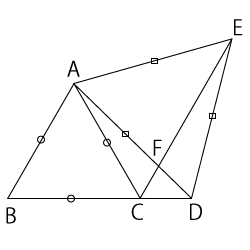
まず、このような証明問題では、長さが等しい辺や角度が等しい角に印をつけるようにしましょう。この問題では、$△ABC$と$△ADE$が正三角形だということが言われてますから、この三角形の辺の長さはそれぞれ等しいです。右の図のように印をつけることができますね。
それ以外は、特に「この辺とこの辺が等しい」とか「こことここの角が等しい」というような内容は書かれてませんから、これ以上印をつけることができません。そのときは、あらためて証明しないといけない2つの三角形にたちかえります。
$△ABD$と$△ACE$について見ると、$AB$と$AC$、$AD$と$AE$それぞれ同じ印がついてますね?そうすると、ちょうど2辺について等しいとわかったわけなんですから、$∠BAD$と$∠CAE$が等しいとわかれば、「2辺とその間の角がそれぞれ等しい」という合同条件を使うことができます。
このように、合同の証明をするときは、等しいとわかっているものを見直して、そこから使えそうな合同条件を導き出すとやりやすいですよ。
さて、$∠BAD$と$∠CAE$についてですが、この2つの角は、よく見るとどっちも$∠CAD$を含んでいますね。このように、重なっている部分がある場合は、何の角と何の角で組み合わさっているか、何の辺と何の辺で組み合わさっているかをもとに考えると、ヒントが見つかる場合があります。
たとえば、今回の問題だと、
\( ∠BAD = ∠BAC+∠CAD \)
\( ∠CAE = ∠EAD+∠CAD \)
というふうに考えます。
ここで、$∠BAC$も$∠EAD$も、どっちも正三角形の角なんですから、これらは絶対に60°です。ということは、$∠BAD$も$∠CAE$も、どっちも\( 60°+∠CAD \)という式になるんで、等しいということになります。
解答のチェックポイント
- 「2辺とその間の角がそれぞれ等しい」という合同条件を利用して証明しているか
- $△ABC$と$△ADE$が正三角形であることを利用して、$△ABD$と$△ACE$の等しい辺を見つけているか
- $∠BAD$と$∠CAE$は\( 60°+∠CAD \)であることを述べているか
答え(解答例).
$△ABD$と$△ACE$において、
$△ABC$は正三角形なので、\( AB = AC \)…①
$△ADE$は正三角形なので、\( AD = AE \)…②
$∠BAD$も$∠CAE$において、
\( ∠BAD = ∠BAC+∠CAD \)…③
\( ∠CAE = ∠EAD+∠CAD \)…④
$△ABC$と$△ADE$は正三角形なので、
\( ∠BAC = ∠EAD = 60° \)
これを、③と④に代入すると、
\( ∠BAD = 60°+∠CAD = ∠CAE \)…⑤
①,②,⑤より、2辺とその間の角がそれぞれ等しいので、
$△ABD$≡$△ACE$