この問題のポイント
体積=たて×横×高さという公式を利用し、たて・横・高さがそれぞれどの辺にあたるかを慎重に判断しよう!
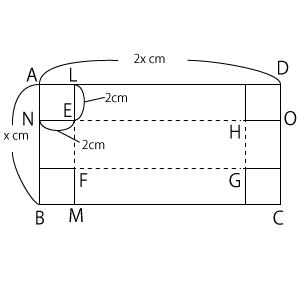
(1)$EF$の長さは、右の図で考えると、$AB$の長さから$LE$、$FM$の長さをひけば求まります。$LE$も$FM$も、切り取った正方形の辺の長さですから、
$EF$
\( = AB-LE-FM \)
\( = x-2-2 \)
\( = x-4 \)(cm)
(2)容器の体積はたて×横×高さで求めることができますから、それぞれの長さをどう表せばよいかを考えましょう。
容器の底面は長方形$EFGH$ですから、たては$EF$、横は$EH$とみなせばよいでしょう。
$EF$の長さは(1)で求めたとおり、$x-4$ですね。
$EH$の長さは(1)で求めたのと同じやり方で考えれば、$AD$の長さから$NE$、$HO$の長さをひけば、
$EH$
\( = AD-NE-HO \)
\( = 2x-2-2 \)
\( = 2x-4 \)(cm)
高さについては、$LE$(切り取った正方形1辺の長さ)と等しいとみなすことができますから、2cmです。
よって、体積は、
\( EF×EH×LE \)
\( = (x-4)(2x-4)×2 \)
\( = 2(x-4)(2x-4) \)
\( = 2(2x^2-12x+16) \)
\( = 4x^2-24x+32 \)(cm3)
(3)(2)で体積を$x$を使った式であらわしました。これが96になればいいんですから、
\( 4x^2-24x+32 = 96 \)
\( 4x^2-24x-64 = 0 \)
両辺を4でわって、
\( x^2-6x-16 = 0 \)
\( (x-8)(x+2) = 0 \)
よって、\( x-8 = 0 \)か\( x+2 = 0 \)になればこの方程式が成り立つんですから、
\( x = 8,-2 \)
「$x$>4とします」という条件が問題文にありましたから、条件に合うのは
\( x = 8 \)
答え.
(1) \( x-4 \)(cm)
(2) \( 4x^2-24x+32 \)(cm3)
(3) \( x = 8 \)