中学数学の問題演習
一次関数と面積
※過去の沖縄県の公立高校入試問題で出題された問題です。
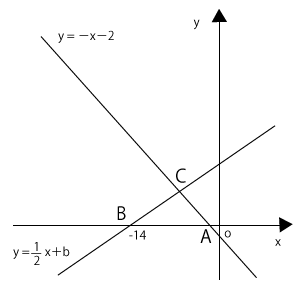
右の図のように、直線\( y = -x-2 \)と直線\( \displaystyle y = \frac{1}{2}x+b \)がある。
この2直線と$x$軸との交点をそれぞれ $A$,\( B(-14,0) \)とするとき、次の各問いに答えなさい。
問1 直線\( \displaystyle y = \frac{1}{2}x+b \)の切片$b$の値を求めなさい。
(半角で入力すること)
問2 直線\( y = -x-2 \)と直線\( \displaystyle y = \frac{1}{2}x+b \)の交点$C$の座標を求めなさい(半角で入力すること)。
問3 点$C$を通り、切片が正の数となる直線を$l$とする。
直線$l$と直線\( y = -x-2 \)と$y$軸とで囲まれた三角形の面積が、△$ABC$の面積と等しくなるように、直線$l$の式を求めなさい。
(半角で入力すること。答えに分数が含まれる場合は、たとえば「5分の1エックス」を入力する場合は「x/5」、「3分の2エックス」を入力する場合は「2x/3」のように入力すること)
統計の代表値
※過去の徳島県の公立高校入試問題で出題された問題です。
| 冊数(冊) | 度数(人) |
| 0 | 2 |
| 1 | 8 |
| 2 | 9 |
| 3 | 10 |
| 4 | 4 |
| 5 | 2 |
| 計 | 35 |
右の表は、35人の生徒が1か月間に読んだ本の冊数を調べ、整理したものである。平均値、中央値、最頻値をそれぞれ求めなさい。ただし、割り切れない場合は、小数第二位を四捨五入して、小数第一位まで求めなさい。(すべて半角で入力すること)
円周角と中心角
※過去の北海道の公立高校入試問題で出題された問題です。
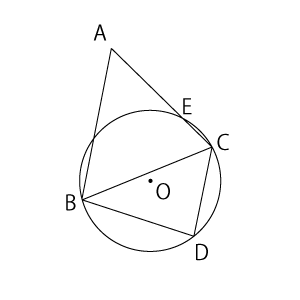
右の図のように、辺$BC$が共通な△$ABC$と△$CBD$がある。$AB$//$CD$とする。3点$C$,$B$,$D$を通る円$O$と、辺$AC$の交点を$E$とする。
次の問いに答えなさい。
(1)$∠BCD$ = 46°のとき、$∠ODB$の大きさを求めなさい。(半角数字で入力すること)
(2)△$ABC$∽△$BED$を証明しなさい。
2けたの数と文字式
※立命館高校の入試問題を参考に作られています。
2けたの自然数$n$の、十の位の数を$a$、一の位の数を$b$とする。等式$n = 4(a+b)$を満たす$n$のうち、最も大きいものを求めなさい。
反比例の式
次の各問いに答えなさい。
(1)$y$は$x$に反比例していて、$x = 2$のとき$y = 1+p$、$x = 4$のとき$y = 2+p$である。このとき、$y$を$x$の式で表しなさい。
(分数を使って答える場合は、たとえば「3分の1」と表記したい場合は「1/3」と記入すること)
(2)$y+5$は$x-2$に反比例していて、$x = 5$のとき$y = 9$である。$x = -5$のときは$y$の値はいくらになるか求めなさい。
