この問題のポイント
次の2つの定理は解くときによく使うから覚えておこう!
・中心角は円周角の2倍の大きさ
・同じ弧に対する円周角はすべて等しい
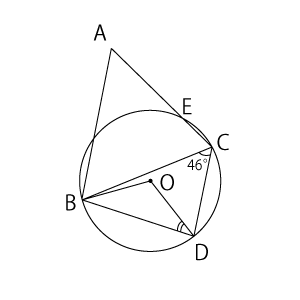
(1)$∠ODB$の角度を求めるんですから、$OD$に線をひきましょう。これだけだと、まだ問題を解ける気がしないですよね?というわけで、中心角は円周角の2倍ということを利用できないかを考えてみましょう。
今わかっている角度は$∠BCD$しかありません。これは弧$BD$に対する円周角ですから、弧$BD$に対する中心角ができるように$OB$に線をひきます。すると、右の図のようになります。
さっきも書いたとおり、中心角は円周角の2倍なんですから、
$∠BOD$ = 46×2 = 92°
求めないといけないのは、$∠ODB$の角度ですが、ここで$OD$,$OB$に線をひいたんで△$OBD$ができていることに気づきませんか?この三角形で考えると、$∠ODB$が求まりそうですから、それで考えてみましょう。
△$OBD$で、$OD$と$OB$は、同じ円の半径なんですから長さは同じはずです。ということは、この三角形は二等辺三角形です。ということは、$∠ODB$と$∠OBD$は等しいですね。
$∠BOD$は92°です。三角形の内角の和は180°ですから、そこから$∠BOD$の角度をひいた残りを半分ずつに分ければいいことになります。よって、
$∠ODB$ = (180°-92°)÷2 = 44°
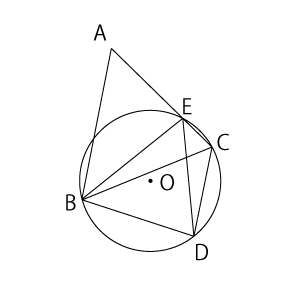
(2)△$BED$とあるので、$BD$と$BE$を右の図のように結んで考えましょう。相似を証明するんですから、相似条件を使いますね。この問題で、辺の長さについてのことは全然書いていませんから、「2組の角がそれぞれ等しい」というものしか使えないと考えて間違いないでしょう。
このような円が関係している問題では、同じ弧に対して円周角がいくつもあるパターンが多いです。「この弧に対しての円周角は…」と考えてできるだけ多くの円周角を見つけましょう。
さらに$AB$と$CD$は平行なんですから、この部分に関しては同位角か錯角を使わないと証明ができないということも頭に入れておかないといけません。
解答のチェックポイント
- $∠ACB$と$∠BDE$が等しいことを円周角を利用して示しているか
- $∠ABC$と$∠BED$が等しいことを、円周角と錯角を利用して示しているか
- 相似条件として「2組の角がそれぞれ等しい」ということを利用しているか
答え.
(1)44°
(2)
弧$BE$に対する円周角なので、$∠ACB$ = $∠BDE$…①
弧$BD$に対する円周角なので、$∠BED$ = $∠BCD$…②
$AB$//$CD$なので、$∠BCD$ = $∠ABC$…③
②,③より、$∠ABC$ = $∠BED$…④
①,④より、2組の角がそれぞれ等しいので、
△$ABC$∽△$BED$