この問題のポイント
交点の座標はグラフの方程式を連立方程式にして求める!
面積は、x軸やy軸上の辺を底辺か高さにして考えるのが基本!
問1 問題文や図からわかるとおり、直線\( \displaystyle y = \frac{1}{2}x+b \)は、\( B(-14,0) \)を通っています。ですから、この方程式に\( x = -14 \),\( y = 0 \)を代入してもOKですから、
\( \displaystyle 0 = \frac{1}{2}×(-14)+b \)
\( 0 = -7+b \)
よって、\( b = 7 \)です。
問2 問1で\( b = 7 \)と求まったんですから、\( y = -x-2 \)と\( \displaystyle y = \frac{1}{2}x+7 \)の2つの交点の座標を求めればいいということになります。
グラフの交点の座標は、直線の方程式を連立方程式にして解くと求められます。ここでは、\( y = -x-2 \)と\( \displaystyle y = \frac{1}{2}x+7 \)を連立方程式にして、これの$x$と$y$の値を求めればいいということになりますね。
今回の方程式は、\( \displaystyle -x-2 = \frac{1}{2}x+7 \)になります。この両辺に2をかけると、
\( -2x-4 = x+14 \)
\( -2x-x = 14+4 \)
\( -3x = 18 \)
\( x = -6 \)
これを\( y = -x-2 \)に代入すると、
\( y = -(-6)-2 = 6-2 = 4 \)
\( x = -6 \)なのでこれが$x$座標、\( y = 4 \)なのでこれが$y$座標ということで、交点$C$の座標は\( C(-6,4) \)となります。
問3 「△$ABC$の面積と等しくなるように」とあるので、△$ABC$の面積がどれほどかを知らないと考えにくいですね。それを求めることから考えてみましょう。
三角形の面積は底辺×高さ÷2で求められます。そして、今回のような関数のグラフを使った三角形の面積のポイントは、$x$軸や$y$軸上の辺を底辺か高さにするということです。
△$ABC$については、辺$AB$が$x$軸と重なっていますね。これを底辺としましょう。$A$の座標は\( y = -x-2 \)と$x$軸との交点ですから、これに\( y = 0 \)を代入すると、
\( 0 = -x-2 \)
これを解くと、\( x = -2 \)ですから、\( A(-2,0) \)。
$B$の座標は\( B(-14,0) \)ですから、$AB$の長さは-2-(-14) = 12。だから、△$ABC$の底辺は12ですね。
一方、高さはどうかというと、$AB$が底辺なんですから、$C$からまっすぐ$AB$に垂線をおろした直線が高さになります。その長さはちょうど$C$の$y$座標と等しくなりますね。ということは、高さは4です。
よって、△$ABC$の面積は12×4÷2 = 24です。このように、$x$軸や$y$軸上の辺を利用すると、どこかの点の$x$座標や$y$座標が利用できてとても便利になります。
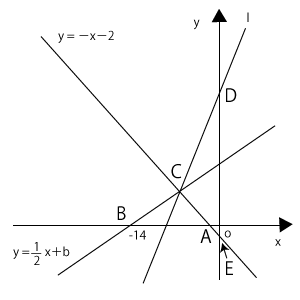
さて、△$ABC$の面積は24ですから、「直線$l$と直線\( y = -x-2 \)と$y$軸とで囲まれた三角形の面積」も24にしないといけません。ここで、右の図のように点$D$と点$E$をとるとしましょう。「直線$l$と直線\( y = -x-2 \)と$y$軸とで囲まれた三角形の面積」とは、△$CDE$のことです。この三角形については$DE$が$y$軸の上にありますから、これを底辺としましょう。
そう考えると、高さは、$C$からまっすぐ$DE$に垂線をおろした直線になり、その長さは$C$の$x$座標が-6ですから6ということになります。
すると、
(底辺)×6÷2 = 24とならないといけませんから、
(底辺)×3 = 24で、
底辺の長さは8にならないといけません。
つまり、$DE$ = 8とならないといけませんが、点$E$は、\( y = -x-2 \)の切片ですから、$E$の座標は(0,-2)です。
ということは、点$D$の座標は(0,6)となれば6-(-2) = 8となって$DE$ = 8となります。この(0,6)というのは、「切片が正の数」という条件にもちゃんと合いますね。
これで直線$l$の切片が(0,6)とわかりましたから、直線$l$の方程式は\( y = ax+6 \)とおくことができます。
しかもこの直線は点$C$を通るんですから、(-6,4)を通ります。ですから、\( x = -6 \),\( y = 4 \)を代入してもOKなんですから、
\( 4 = -6a+6 \)
これを解くと、\( 6a = 6-4 \)
\( 6a = 2 \)
\( \displaystyle a = \frac{1}{3} \)
だから、直線$l$の方程式は、\( \displaystyle y = \frac{1}{3}x+6 \) です。
答え.
問1 \( b = 7 \)
問2 \( C(-6,4) \)
問3 \( \displaystyle y = \frac{1}{3}x+6 \)