中学数学の問題演習
令和6年2月27日
一次関数と速さ・距離
※東京都の成城学園高校の入試問題です。
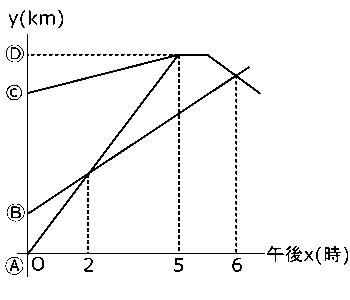
Ⓐ地からA君が、Ⓑ地からB君が、Ⓒ地からC君が午後0時に出発してⒹ地に向かう。右の図は、Ⓐ地からの道のりと時間との関係を表したものである。ここで、A君,B君,C君の速さの比は5:3:1であり、Ⓑ地とⒸ地の間の道のりは32kmである。
午後2時にB君はA君に追い越され、午後5時にA君とC君は同時にⒹ地に着いた。
ただしⒶ地からⒹ地までは一本道で、Ⓐ地,Ⓑ地,Ⓒ地,Ⓓ地の順にあるものとする。次の問いに答えなさい。
(1)C君がⒹ地に向かうときの速さを毎時$a$kmとし、Ⓐ地とⒷ地の間の道のりを$b$kmとしたとき、$a$,$b$の値を求めよ。(半角数字のみ入力すること)
(2)A君が、B君の位置とC君の位置のちょうど真ん中の位置にくるのは午後何時何分か。(半角数字のみ入力し、分の数値が0~9の1けたの場合は00~09の2けた表記で入力すること)
(3)C君はⒹ地で休んだ後、Ⓒ地へ毎時8kmの速さで同じ道を戻った。途中、B君と午後6時にすれ違った。C君は何分間休んだか。(半角数字のみ入力すること)
令和5年11月22日
立方体の切断面
※茨城県の茗溪学園高校の入試問題を参考に作られています。(数字は半角で入力すること)
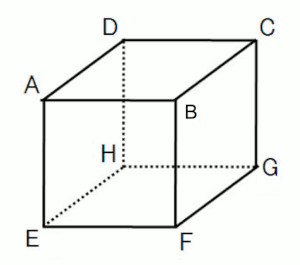
1辺の長さが6cmの立方体$ABCD$-$EFGH$があり、辺$EF$,$FG$の中点をそれぞれ$M$,$N$とする。点$P$は$F$を出発して毎秒1cmの速さで辺上を$B$,$C$,$D$を経由して$H$まで進むものとする。3点$M$,$N$,$P$を通る平面でこの立方体を切ったとき、次の問いに答えなさい。
(1)切り口の図形は$n$角形となる。$n$にあてはまる整数をすべて求めよ。
(2)切り口が正三角形になるのは、点$P$が$F$を出発してから何秒後か求めよ。
(3)切り口が正六角形になるのは、点$P$が$F$を出発してから何秒後か求めよ。
(4)点$P$が$F$を出発してから11秒後の切り口の形を答えよ。
令和5年8月16日
円周角の定理の逆
※東京都の豊島岡女子学園高校の入試問題です。
- 半角で入力すること。根号の√は「ルート」で変換して出るものを入力すること。
- 分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること。
- 無理数は、たとえば「ルート3」なら√3のように、√につづけて入力すること。
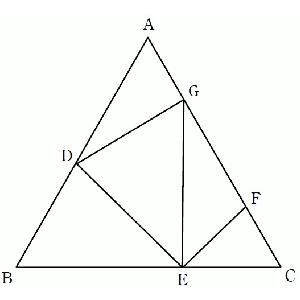
右の図の正三角形$ABC$において、$△BDE$≡$△GDE$,$AG$ = $CF$ = 1,$AD$ = 2となるように、辺$AB$,$BC$上にそれぞれ点$D$,$E$を、辺$CA$上に2点$F$,$G$をとります。
(1)$∠DEG$の大きさを求めなさい。
(2)$FG$の長さを求めなさい。
(3)3点$E$,$F$,$G$を通る円の半径を求めなさい。
令和5年5月18日
数え上げ方と確率
※( )内の入試問題で出題された問題です。(半角のみで入力し、分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること)
(1)5本のくじの中に3本の当たりくじが入っている。
(東京・日本大第一)
① 同時に2本引くとき、2本とも当たりくじである確率を求めなさい。
② Aさんが先に1本引き、残りの中からBさんが1本引くとき、AさんがはずれBさんが当たる確率を求めなさい。
(2)-1,0,1,2,3の数字を1つずつ書いた5個の玉を入れた袋がある。この中から玉を1個取り出して数字を調べ、それを袋に戻してから、また玉を1個取り出すとき、取り出した2個の玉の数字の積が正となる確率を求めなさい。また、この袋から玉を同時に2個取り出すとき、2個の玉の数字の積が負となる確率を求めなさい。
(愛知・名城大附)
(3)袋の中に、赤玉3個,白玉2個が入っている。そこから同時に2個を取り出すとき、2個とも同じ色である確率を求めなさい。
(東京・日本大豊山女子)
(4)袋の中に赤玉,青玉,黄玉が各色2個ずつ合わせて6個入っており、同じ色の2個の玉には、一方に1,もう一方に2の数字が書いてある。この袋の中から玉を1個取り出し、玉の色と、書いてある数字を記録して、もとに戻す。もう一度袋の中から玉を1個取り出し、玉の色と、書いてある数字を記録する。1回目に取り出した玉と2回目に取り出した玉について、色が異なり数字が一致する確率を求めなさい。ただし、どの玉を取り出す確率もすべて等しいものとする。
(東京都立国分寺)
令和5年2月7日
食塩水の濃度と一次方程式
※城北埼玉高校の入試問題です。
※入力は次の指示にしたがってください。
- 半角のみで入力すること。分数は、たとえば分母が5で分子が2なら[2]/[5]のように、それぞれを[]で囲って(分子)/(分母)の形で入力すること。
- $●x+■$という形の式で●や■にあたる部分が分数になる場合、\( \displaystyle \frac{◆x+▲}{〇} \)のように、一つの分数にまとめること。そして、たとえば分母が3で分子が2x+4なら[2x+4]/[3]のように、分母と分子それぞれを[]で囲むこと。
容器Aには濃度$x$%の食塩水が100g入っている。容器Aから別の空の容器に50gを移し、それに濃度10%の食塩水50gを加えてよくかきまぜ、そこから50gを容器Aに戻して、よくかきまぜる、という操作をくり返し行う。
(1)1回の操作後の容器Aの食塩水の濃度を$x$で表せ。
(2)2回の操作後の容器Aの食塩水の濃度を$x$で表せ。
(3)3回の操作後、Aの濃度は8.5%となった。$x$の値を分数で求めよ。
